Podemos considerar que una animación describe
cómo cambia una imagen a lo largo del tiempo, con el suficiente
número de fotogramas por segundo para dar un efecto de
continuidad.Existen diversas técnicas que intentan conseguir
este objetivo. A grandes rasgos podemos dividirlas en dos, las
de animación clásica y las de animación de
síntesis por ordenador, que puede basarse en una representación
2D ó 3D de los objetos (aunque el resultado final será
obviamente bidimensional).
La animación clásica, que ahora
podríamos llamar de tipo raster, genera la secuencia
de imágenes por métodos pictóricos, lo que
entendemos por una imagen "dibujada", formada por pixels
cuya coloración se asigna manualmente o por mecanismos
sencillos guiados de forma manual (por ejemplo, sistemas de relleno
automático). No emplea ningún tipo de síntesis
automática para conseguir efectos de profundidad y perspectiva,
sino que es una labor de los dibujantes conseguirlos manualmente.
Las imágenes deben generarse una por una, aunque esta tarea
suele distribuirse en varios niveles; separando el dibujo de momentos
claves en la acción de los personajes, el dibujo de los
fondos (que usualmente no cambian de un fotograma a otro) y las
tareas de interpolación y coloreado de cada imagen.
La animación de síntesis por ordenador
crea las imágenes por un proceso automático a partir
de una especificación o modelado de los objetos que forman
parte de la escena y de su movimiento. Este modelo de los objetos
puede ser bidimensional, con lo cual el resultado se parece más
a la animación tradicional, o puede basarse en un modelo
3D, donde pueden aplicarse métodos realistas de sombreado,
simulación física, etc.
En este curso vamos a centrarnos en las distintas
técnicas de animación sintética 3D, basándonos
en los conocimientos sobre representación de objetos y
visualización que ya hemos desarrollado. Tenemos que describir,
por tanto, qué técnicas son utilizadas para describir
los cambios de todo tipo que sufre una escena tridimensional a
lo largo del tiempo. Una animación de síntesis siempre
funciona evaluando el estado de la escena para el instante correspondiente
a cada fotograma y visualizándola por alguno de los métodos
existentes.
Si los fotogramas se van generando a partir de una
especificación previa y se van almacenando el ficheros
(o en un fichero único para toda la animación) hablaremos
de una animación fotograma a fotograma u animación
off-line. Esta es la única forma de conseguir animaciones
finales de gran calidad, donde el tiempo de cómputo de
cada fotograma puede oscilar entre unos pocos segundos y varias
horas.
Una situación diferente se produce cuando
el proceso que crea la animación va mostrando los fotogramas
inmediatamente después de producirlos, permitiendo al usuario
efectuar cambios sobre la marcha. En este caso, que podríamos
llamar animación interactiva o animación
on-line, la frecuencia de presentación de las imágenes
viene determinada por su velocidad de cómputo de las imágenes,
o sea, por la potencia del equipo que las calcula y la complejidad
de la escena.
Si en la animación interactiva conseguimos
que la velocidad aparente de los procesos representados sea equivalente
a la de la realidad hablaremos de animación en tiempo
real, concepto que desarrollaremos en el siguiente tema, y
si además se desarrolla algún tipo de simulación
encargada de actualizar el estado de la escena en cada momento
teniendo en cuenta posiblemente las acciones del usuario del programa
(por ejemplo, mover el ratón para indicar en qué
dirección quiere moverse), entonces hablaremos de simulación
en tiempo real.
5.1 TÉCNICAS DE FOTOGRAMAS CLAVE O KEYFRAMES
Este tipo de técnicas son una trasposición
basante directa de los métodos de la animación tradicional
para describir los cambios temporales de la escena. La idea básica
consiste en definir mediante edición manual o mediante
alguna función automática cuál es el estado
de la escena en ciertos instantes (fotogramas clave o keyframes),
incluyendo la posición de los objetos y fuentes de luz,
sus propiedades, y también la posición y características
del observador o cámara. Se continua así con la
idea de la animación tradicional en la que el dibujante
'experto' traza en blanco y negro las siluetas de los personajes
en los momentos clave, para que posteriormente los interpoladores
se encarguen de generar las imágenes intermedias. En la
animación de síntesis la interpolación en
el tiempo se efectuará a partir de los valores que determinan
los fotogramas clave (posiciones, orientaciones, velocidades,
propiedades…) mediante algún algoritmo automático.
Este proceso de interpolación es clave, ya que debe producir
un resultado coherente, de apariencia natural (lo que no es nada
fácil, por ejemplo, en los movimientos de figuras articuladas
como el cuerpo humano). No nos interesa que por efecto de la interpolación
en la animación aparezcan saltos bruscos o cambios extraños.
Para conseguir los efectos deseados, el diseñador de la animación puede insertar más fotogramas clave (con menos separación temporal entre ellos) en aquellas partes de la secuencia animada donde necesite hacer una descripción más detallada de los cambios. Además de dar los valores que definen estáticamente cada fotograma clave (p.ej. las posiciones), el diseñador puede también indicar cuál es el valor de ciertas variables dinámicas (p.ej. velocidades), lo que le dará un mayor grado de control sobre la manera en que va a realizarse la interpolación.
La representación más formal de una
animación por keyframes sería una gráfica
como la siguiente, en la que aparecen los valores de cada una
de las variables que definen la escena y su variación con
el tiempo. Este diagrama se llama diagrama de movimiento
o motion graph:
Asociado al diagrama básico que muestra la
evolución de las variables con el tiempo podemos tener
otros gráficos en los que unas variables se representan
en función otras variables. Por ejemplo, la trayectoria
de un móvil puede verse únicamente en función
de sus componentes espaciales (ver figura a la izquierda) o a
través de la relación de ambas coordenadas espaciales
con el tiempo (ver a la derecha):
Podríamos pensar que a partir de la representación
espacial de la trayectoria podemos averiguar la velocidad del
movimiento, observando la distancia entre dos posiciones correspondientes
a keyframes consecutivos. Pero esto no es cierto, ya que el objeto
no tiene porqué moverse a velocidad constante sobre la
trayectoria. La velocidad instantánea real vendrá
dada por las pendientes de las gráficas de las posiciones
en el diagrama de movimiento. Así, el vector velocidad
instantáneo será 
, y su
módulo será la velocidad de traslación sobre
la trayectoria.
Para construir los valores intermedios de las variables
a partir de los keyframes necesitamos una función de interpolación
con buenas propiedades, y a la vez poco costosa de evaluar. Se
suelen emplear curvas paramétricas, ya que tienen un comportamiento
suave y son controlables (como se comentó, cumplen la propiedad
de la envolvente convexa).
Hagamos un repaso de los tipos de curvas paramétricas
para comprobar cuáles pueden resultar más convenientes.
Además de estas curvas paramétricas
también se puede emplear una sencilla interpolación
lineal entre los valores de los keyframes. Esto permite resolver
la interpolación mediante un cálculo muy sencillo,
pero se trata de un tipo de ecuación que producirá
cambios bruscos en la derivada de la variable y no permite un
control detallado si no se añaden suficientes keyframes.
Además del tipo de interpolación, resulta
fundamental la elección correcta de los parámetros
a controlar, ya que puede facilitar mucho la tarea de calcular
los valores intermedios. Por ejemplo, una interpolación
lineal de la posición puede ser adecuada para una partícula
que se mueve con una trayectoria suave (ver figura 5.1.(a)). Sin
embargo, si deseamos describir la rotación de un objeto
alrededor de un punto, resultaría poco adecuado hacerlo
con una interpolación lineal de la posición, siendo
mejor hacerlo con una interpolación ,lineal o no, sobre
un ángulo que describe el giro (ver figura 5.1.(b)).
El método de fotogramas clave deja un problema
abierto: cómo realizar la asignación de valores
a las variables en los keyframes. Podemos resolverlo de distintos
modos. Si disponemos de algún método algoritmico
(por ejemplo una simulación basada en ecuaciones físicas)
para calcular el valor de estas variables en el tiempo, entonces
podríamos usarlo para calcular el estado de la escena en
ciertos instantes y luego utilizar la interpolación entre
keyframes. Este sistema puede ser útil cuando el algoritmo
exacto resultaría demasiado costoso de tener que utilizarlo
para cada fotograma aislado y resulta conveniente hallar estos
por interpolación.
En el caso de que no dispongamos de un algoritmo
o procedimiento automático para calcular la evolución
de las variables de la escena con el tiempo tendremos que recurrir
a otros métodos.
Es el método más creativo para generar
animaciones, asignando de forma manual los valores de las variables
en cada keyframe. Normalmente esta asignación no se realiza
dando directamente los valores numéricos , sino a través
de un sistema gráfico de diseño. Todos los programas
de animación 3D proporcionan interfaces de manipulación
directa que permiten realizar dos tipos de tareas distintas que
pueden combinarse entre sí para garantizar la coherencia:
a) Dada una asignación de valores en los diferentes
keyframes, representar la situación de la escena en los
instantes deseados para observar si el movimiento de los distintos
objetos se aproxima al efecto que queremos conseguir . Es decir,
dispondremos de un modo de 'previsualización' conjunta
de la escena, al menos para instantes concretos de tiempo.
b) Para determinar los keyframes, el interfaz deberá permitirnos dar la secuencia de valores para una variable dada. Para ello podremos manipular cada objeto y sus propiedades hasta colocarlo en el estado deseado y luego asignar este estado a un instante (keyframe) determinado.
A pesar de su flexibilidad y potencia expresiva,
este método manual plantea el problema de la dificultad
para reproducir con naturalidad comportamientos de sistemas complejos,
sistemas donde intervienen actores (personas, animales u objetos
'animados') o sistemas que obedecen a leyes físicas, obteniéndose
a veces resultados poco realistas.
La rotoscopia es una técnica que se basa en
la grabación de los movimientos o comportamientos reales
para la generación de fotogramas clave. Un problema típico
que se resuelve mediante este tipo de práctica sería
la representación de la locomoción y otros movimientos
de los animales. Tradicionalmente, la grabación se realizaba
mediante fotografía o filmación y se copiaba a mano
sobre los dibujos, adaptando la forma de los personajes. Este
sistema ha sido utilizado por la compañía Disney
desde el primer largometraje de dibujos animados (Blancanieves).
Este método se ha extendido a la animación
por ordenador mediante la captura de movimiento
que consiste en introducir directamente en el ordenador variables
numéricas que representarán, por ejemplo, las posiciones
de las articulaciones en ciertos puntos seleccionados.
Los valores de posición se obtiene bien mediante
dispositivos de seguimiento (localizadores o trackers) o bien
por el análisis de imágenes (se viste a la persona
de un color, por ejemplo azul, y se le ponen puntos de otro color
en los lugares cuya posición se debe detectar). De este
modo se consiguen secuencias muy realistas de movimiento, que
luego pueden mezclarse o deformarse en tiempo real (por ejemplo,
los movimientos de los luchadores o jugadores de fútbol
en la última generación de videojuegos).
Una vez asignados los valores que las variables de
la escena van a tener en ciertos instantes, definiendo así
los fotogramas clave, la definición correcta de la interpolación
plantea otro problema, que podríamos denominar el control
de la velocidad. La velocidad, y su derivada la aceleración,
son factores muy importantes del movimiento que le confieren características
de más o menos realismo, por lo que su control resulta
también necesario. Efectos como la inercia de un movimiento
o la acción de fuerzas (empujones, choques, propulsión…)
involucran a la velocidad y la aceleración.
Para poder visualizar estas magnitudes se añaden
nuevos diagramas:
Para obtener efectos adecuados en la animación
debemos controlar también estos diagramas, pero teniendo
en cuenta que se hayan directamente ligados al diagrama de movimiento.
Si hemos definido una trayectoria 
, el
diagrama de velocidad se obtendrá derivando esta función
y el de aceleración derivando una vez más. A su
vez, si especificamos una velocidad inicial, podemos deducir el
diagrama de velocidad integrando la función de aceleración,
y dando la posición inicial calcularemos la trayectoria
integrando la función de velocidad, de manera que podemos
crear trayectorias que cumplan con determinadas especificaciones
de aceleración o velocidad.
5.2 ANIMACIÓN PROCEDURAL Y BASADA EN REGLAS
En estos tipos de animaciones tenemos un método
algorítmico para calcular las variables que definen el
comportamiento de los objetos, de la cámara y otras características
de la escena a lo largo del tiempo. Estos métodos podrán
utilizarse para hallar directamente el estado de la escena en
cada fotograma de la animación final, o bien para asignar
valores a los keyframes y aplicar más tarde un método
de interpolación. La primera variante de funcionamiento
requiere que el algoritmo encargado de calcular la evolución
temporal se ejecute al mismo tiempo que se va generando la animación,
lo que incrementará el coste temporal total. El método
de utilizar los keyframes como representación intermedia
supone realizar una aproximación, pero como contrapartida
permite almacenar el resultado de la simulación para posteriormente
generar los fotogramas necesarios por interpolación, de
manera que el algoritmo exacto ya no resulta necesario durante
el cálculo final de la animación.
En los métodos procedurales
es una función o procedimiento, en el sentido matemático
y computacional, lo que define la evolución del conjunto
de parámetros por medio de una expresión paramétrica
en función del tiempo 
, o bien
por medio de una expresión integral o incremental, también
en función del tiempo: 
.
En los métodos basados en reglas
existe un sistema o conjunto de reglas que determinarán
el valor de los parámetros en cada instante de tiempo.
Las reglas suelen tener la forma básica SI (condición)
ENTONCES acción, pudiendo activarse o no según
la condición sea verdadera o falsa, lo que normalmente
depende del valor del tiempo y de los parámetros en un
instante anterior. La idea es la misma que en el caso procedural;
definir cómo cambian los valores de la escena con el tiempo,
pero ahora este cambio no se puede expresar mediante una función
matemática. Estos métodos basados en reglas se emplean
cuando aparecen discontinuidades en el tiempo (por ejemplo, un
objeto se comporta de determinada manera hasta que llega cerca
de otro, y entonces su movimiento se altera debido a una cierta
decisión). Su aplicación más usual es la
representación de las relaciones complejas, no debidas
a meras interacciones físicas, entre los distintos objetos
de una escena. En algunos casos se llega a hablar de métodos
basados en el conocimiento o métodos de inteligencia
artificial.
El resultado de un sistema de reglas es difícil
de evaluar a simple vista. Habrá situaciones en las que
se dispare más de una regla, y por lo tanto habrá
que dotar de un orden de preferencia a las reglas o especificar
cómo se combinan los resultados de decisiones diferentes
(esto es posible, por ejemplo, en los sistemas basados en lógica
difusa o fuzzy). En algunas ocasiones las reglas pueden
involucrar la eliminación o adición de nuevos elementos
a la escena, lo que también puede provocar problemas de
consistencia.
Existen lenguajes de animación que permiten
representar ambos métodos, tanto el basado en procedimientos
como en reglas, y combinarlos simultáneamente, como los
lenguajes de script o guiones.
Con estos métodos de generación de
comportamientos se pueden simular muchos sistemas naturales (nubes,
fluidos, humo, ... ) como conjuntos de partículas
que interactúan entre sí (analizaremos esta técnica
con más detalle posteriormente). Otra posibilidad consiste
en el actoring; la simulación de objetos animados
complejos que pueden descomponerse en un esqueleto articulado,
incluso con modelos de músculos, que sigue ciertas reglas
físicas y conductuales en su movimiento.
También pueden utilizarse procedimientos y
reglas para controlar las relaciones mutuas de un grupo de objetos
o actores cuando tienen que comportarse de una manera coordinada.
Estas técnicas se han utilizado especialmente para guiar
los movimientos de grupos de animales, sean dinosaurios, peces
o pájaros.
Veamos ahora un ejemplo muy sencillo de animación
procedural. Se trata de un móvil que se desplaza en una
dimensión x a una velocidad constante de diez unidades.
Las versiones paramétrica e incremental de un procedimiento
que devolviera la posición para cada instante serían
:
Procedimientos
const v = 10; const v = 10;
proc_param(t): real proc_increm(x_anterior,
): real
{ return ( v t ); } { return ( x_anterior
+ v 
); }
Para representar la persecución entre un depredador
y su presa en una dimensión podríamos definir el
siguiente modelo basado en la combinación de reglas y cálculos
procedurales:
Reglas
Variables del Depredador : Xd,Vd
Variables de la Presa : Xp,Vp
Procedimiento actualizar_pos_depredador
(
)
{
si Xd -Xp 10 (si la presa se acerca a menos de diez unidades)
Vd = ( Vd + Vp ) 2 se le asigna una velocidad entre la suya y la de la presa
si Xd -Xp >= 10 (si la presa está más lejos)
Vd
= 0 el depredador está parado
si Xd -Xp 0.001 ( si se ha cazado la presa)
Vd = 0; Vp = 0; ambos se paran
Xp
= Xp
+ Vp
se actualiza la posición del depredador
}
La función definida para el depredador incrementa
automáticamente su posición al moverse la presa.
Una función similar podría ser utilizada para el
movimiento de ésta.
Ejemplo:
En la siguiente figura podemos observar un ejemplo
más elaborado, en el que el movimiento de un pájaro
es controlado mediante una serie de variables cuyos valores puede
cambiar el usuario.
Cuando en los procedimientos de movimiento se utiliza
la representación cinética (solamente se
especifican aceleraciones y velocidades, pero no las furerzas
que actúan) o dinámica (se añaden
fuerzas que deben determinar el movimiento) de la física,
se suele hablar de simulación física. Estas
técnicas pueden conllevar diferentes grados de complejidad
computacional según la aproximación elegida. Los
casos más elementales se detallan en los puntos siguientes.
En este caso la variable representativa es la posición
de un punto sin dimensiones. Para no considerar momentos de inercia
ni movimientos de rotación, se supondrá que la masa
de los cuerpos, un dato que tampoco se usa en la simulación,
estará concentrada en un único punto.
Para generar la animación hay que calcular
, normalmente en función de la
velocidad 
y la aceleración 
.
El movimiento vendrá descrito por ecuaciones
diferenciales que relacionarán estas tres funciones. La
forma de resolverlas para hallar el movimiento x(t) se basa en
diferentes métodos de integración.
Consideremos un caso muy sencillo en el que disponemos
de la función de aceleración a(t). A partir de ella
podemos integrar la velocidad y la posición, utilizando
por ejemplo el método de los trapecios.
En este caso el problema de especificar el movimiento
se reducirá a hallar la variación del vector aceleración
con el tiempo.
Es similar al caso anterior, pero ahora debemos tener
en cuenta las fuerzas y la masa del punto en las ecuaciones diferenciales
que ligan la posición, velocidad y aceleración.
Según el tipo de fuerzas que se consideren necesitaremos
conocer distintas propiedades del objeto, como masa, carga eléctrica,
elasticidad, etc. La ecuación básica es 
,
a partir de la cual se podría calcular la aceleración
del punto, y por tanto la velocidad y la posición. Sin
embargo, debe tenerse en cuenta que la fuerza puede depender a
su vez de la posición (por ejemplo, las fuerzas elásticas)
o la velocidad (fuerzas de rozamiento, fuerzas magnéticas
sobre cargas eléctricas). También podemos considerar
en nuestro modelo fuerzas impulsivas, debidas a choques
o contactos temporales con otros cuerpos, que pueden modificar
bruscamente la velocidad y dirección de movimiento del
punto. Reorganizando la fórmula anterior podemos deducir
el cambio de velocidad producido por una fuerza que actúa
durante un tiempo 
: 
Por otro lado las fuerzas pueden estar generadas
por un campo de fuerzas que actúa sobre alguna magnitud
activa (masa, carga) del objeto, por ejemplo el campo gravitatorio
generado por otros cuerpos.
5.3.3 CINEMÁTICA DE UN SÓLIDO RÍGIDO
La diferencia entre el modelo de sólido rígido
y el del punto material es la introducción de la extensión
del cuerpo, y por tanto de un nuevo comportamiento: la rotación
alrededor de su centro de masas. Al movimiento propio del centro
de masas pueden aplicarse las mismas ecuaciones que del modelo
puntual. Pero además hay que describir la rotación.
Ésta puede ser muy compleja, puesto que existen tres grados
de libertad, y en principio habría que describir la evolución
de tres ángulos de giro independientes. Sin embargo, en
muchos casos podemos reducir el giro a un movimiento alrededor
de un eje, y por tanto descrito por un único ángulo.
El ángulo juega el mismo papel que la posición en
las ecuaciones cinemáticas, donde no aparecen fuerzas.
Denominando 
al ángulo de giro
tenemos:
Velocidad angular: 
Aceleración
angular: 
5.3.4 DINÁMICA DEL SÓLIDO RÍGIDO
Las fuerzas actúan sobre el centro de masas
del sólido rígido de la misma forma que sobre el
punto material, pero las fuerzas impulsivas (y otras, como las
magnéticas) influyen en el posible giro del objeto. En
relación con la dinámica de rotación, el
momento de inercia (en principio es una matriz 3x3) hace el papel
equivalente a la masa, y el momento de una fuerza sustituye a
las fuerzas. El momento de una fuerza se define como el producto
vectorial entre la fuerza aplicada al objeto y el vector de posición
del punto en que se aplica (
).
Si el giro se produce alrededor de un eje fijo, 
se convierte en un escalar, obteniendo: 
En una colisión elástica en
la que no actúan fuerzas externas, además de conservarse
la cantidad de movimiento total (masa por vector velocidad) también
se conserva la energía cinética total 
si no actúan fuerzas. De esta manera, en un sistema donde
solamente hay colisiones elásticas no se pierde energía
y los objetos siguen moviéndose indefinidamente.
En una colisión inelástica sí
existe perdida de energía cinética, que es absorbida
por los cuerpos que chocan. Las colisiones reales siempre suponen
la pérdida de alguna energía.
Resulta complicado desarrollar un buen modelo de
colisión, ya que éste implica calcular con precisión
el punto de contacto entre los cuerpos y resolver las condiciones
impuestas por los principios de conservación y la posible
pérdida de energía (incluyendo en el caso real las
deformaciones que pueden sufrir los cuerpos). Si suponemos un
comportamiento elástico y un punto de contacto en el que
uno de los objetos puede aproximarse como una superficie localmente
plana y el otro como un punto podemos desarrollar un modelo sencillo,
que serviría, por ejemplo para representar el rebote de
una pelota contra una pared o suelo.
Existen sistemas donde la interacción es mucho
más compleja y no puede reducirse a una colisión
clásica. Un ejemplo es el comportamiento de una tela que
cubre a un cuerpo humano. Su movimiento depende de la fuerza de
la gravedad, del contacto con la forma geométrica del cuerpo
y de las características elásticas de la superficie
de la tela.
Independientemente del modelo físico que utilicemos
para representar los objetos individuales, debemos estudiar cómo
vamos a organizar el cálculo del comportamiento físico
en aquellos sistemas que están formados por un conjunto
de cuerpos, como por ejemplo el Sistema Solar. Como es frecuente,
deberemos llegar a un compromiso entre la fidelidad de la representación
y el coste computacional, recurriendo a diferentes tipos de aproximaciones.
Esta sería la aproximación más
sencilla y menos costosa, en la que consideramos que los diferentes
objetos no se relacionan entre sí, o que lo hacen solamente
en momentos determinados. Incluso con un método tan sencillo
es posible representar de forma realista fenómenos complejos,
como ciertos procesos naturales (gases, ciertos flujos de líquidos
-una cascada de agua-, humo. etc.).
Si queremos simular una cascada de agua podemos,
por ejemplo, suponer que cada partícula se comporta como
un punto material, e ir generándolas de forma aleatoria
a partir de una fuente, caracterizándolas mediante varias
distribuciones estadísticas que nos den la probabilidad
de los ángulos de salida a partir de la fuente y de la
velocidad inicial: P(), P(),
P(v0)
Es fácil comprender que en todos los sistemas
de partículas independientes el coste computacional sería
de orden lineal 
, siendo n el número
de partículas.
Diremos que dos partículas están relacionadas
mediante una ligadura flexible cuando existe una fuerza entre
ellas, pero no hay una restricción en los grados de libertad
de la posición de ambas. Veremos más adelante que
existen otro tipo de ligaduras no flexibles, en las que los cuerpos
pueden estar unidos mediante articulaciones, apareciendo restricciones
en el movimiento.
a) Inestructuradas :
Cada una de las partículas interactúa con todas las demás. Esto sucede con la fuerza gravitatoria y otras fuerzas de largo alcance. En una simulación del Sistema Solar tendríamos en principio que considerar las fuerzas que actúan entre cada par de cuerpos i, j:
El problema de considerar todas estas interacciones
es que el número de cálculos a realizar tiene un
coste cuadrático 
con el número
de partículas.
b) Estructuradas :
En este caso se supone que las partículas
solamente interactúan con un conjunto finito de sus vecinas.
Esto sucede cuando las partículas forman parte de una estructura
que limita el alcance de las fuerzas, como sucede entre las moléculas
de un líquido o un sólido. Si suponemos que el número
de vecinas a considerar es más o menos constante (k),
el coste de cálculo de las interacciones sería de
nuevo lineal con el número de partículas: 
.
Incluso puede utilizarse esta aproximación para simular
sistemas en los que la vecindad entre partículas puede
cambiar (por ejemplo en un fluido muy viscoso o gel hay una cierta
estructuración, pero ésta puede cambiar con el tiempo).
Ejemplo : Estructura
molecular con potencial atractivo-repulsivo. Un ejemplo de este
tipo de sistemas serían los sólidos, y si permitimos
que haya cambio en el grupo de partículas vecinas podríamos
también considerar líquidos, espuma, etc.
La relación entre la fuerza F y el potencial
V es: 
, y un ejemplo de cómo serían
este tipo de magnitudes dependiendo de la distancia entre las
partículas podría ser:
5.4 LIGADURAS RESTRICTIVAS Y FIGURAS ARTICULADAS
Un concepto de ligadura diferente al de ligadura
flexible aparece cuando dos objetos se relacionan por medio de
fuerzas y además existe una limitación en los movimientos
debido a esa unión. Llamaremos a este tipo de relación
ligadura no flexible, ligadura con restricciones o ligadura
rígida. En este caso se produce una disminución
en los grados de libertad del movimiento de los cuerpos.
El número de grados de libertad es la cantidad
mínima de variables necesarias para especificar exactamente
la posición de un objeto. Si un objeto no está sometido
a ningún tipo de restricción, tiene seis grados
de libertad: tres variables (coordenadas espaciales) para determinar
su localización, y otras tres (ángulos) para determinar
su orientación. Nótese que este número no
varía aunque cambiemos el tipo de sistema de coordenadas
(las tres coordenadas espaciales pueden ser cartesianas, esféricas
o de cualquier otro tipo, pero siempre harán falta tres).
Cuando aparece una ligadura rígida este número
disminuye. Por ejemplo, si sujetamos el objeto a una bisagra estática
eliminamos todos los grados de libertad de posición y solamente
dejamos un grado de libertad de rotación.
En muchos programas de animación y simulación
existe la posibilidad de establecer este tipo de ligaduras entre
diferentes objetos y aprovecharlas para producir animaciones.
Para establecer una ligadura rígida se suelen definir funciones
de transferencia entre variables de diferentes objetos. Por
ejemplo, podemos especificar que la posición en x
de un objeto se relacione con el ángulo de giro 
de otro objeto por medio de la función 
.
Esta función debe actuar haciendo que si en cualquier momento
cambia el valor de x, el valor de 
variará
según esta relación.
En este ejemplo, a partir del giro del cilindro se
determinaría mediante una función el valor de la
translación en z del cubo.
Habrán ligaduras reversibles cuando
la función es estrictamente creciente o decreciente, y
por tanto existe una correspondencia biunívoca entre ambos
grados de libertad. En nuestro ejemplo significaría que
a partir de trasladar z se pueda obtener giro x
y también a la inversa. Pero también pueden ser
no reversibles. En caso de que la función no sea
siempre creciente o decreciente, como sucede en la gráfica
del ejemplo, no podemos hallar la relación inversa. En
el ejemplo se puede ver que a un determinado valor de 'trasladar
z' podrían corresponder dos valores diferentes de 'giro
x', y por tanto no existiría una función inversa.
Pero establecer una relación de ligadura no
especifica cómo ambas variables van a cambiar con el tiempo.
Por esta razón se suelen añadir los llamados generadores
de funciones temporales, que podemos imaginar como procedimientos
que dan como salida un cierto valor que es función del
tiempo (por ejemplo una función lineal o sinusoidal). En
algunos entornos para el desarrollo de animaciones existe una
representación gráfica de las funciones de transferencia
y de los generadores temporales como bloques que se pueden conectar
entre sí y con los parámetros de los objetos para
especificar la animación (VER FIGURA). En otros no existe
este entorno gráfico, pero sí las estructuras y
funciones necesarias (como en el entorno de desarrollo dVise de
Division Ltd. o en la librería gráfica IRIS Inventor.
Otra técnica posible es definir grados de
libertad o parámetros virtuales. En lugar de utilizar
un grado de libertad de un objeto para controlar otro, puede crearse
un nuevo parámetro que no corresponde a ningún objeto
particular pero que sirve para controlar a uno o más grados
de libertad reales de los objetos. Esta es una manera sencilla
de coordinar los movimientos de diferentes partes de un objeto
o de relacionar un objeto con otro. Las ligaduras por medio de
parámetros reales y virtuales pueden anidarse, creándose
una jerarquía de ligaduras, de manera que con pocas variables
pueden controlarse un gran número de grados de libertad
de la escena.
En este ejemplo se han definido dos parámetros
virtuales (p1 y p2) que permiten, a través de cuatro funciones,
controla de forma coordinada las posiciones de los dos ojos y
la boca mediante el valor de p1.
Una jerarquía articulada es un conjunto de
partes rígidas que están unidas dos a dos por medio
de ligaduras restrictivas llamadas articulaciones. Este
tipo de sistemas (que la Robótica estudia en profundidad)
no tienen en principio grados de libertad relacionados con la
posición, sino solamente con las rotaciones (de una hasta
tres dependiendo del tipo de articulación). Sin embargo,
puesto que los objetos visuales no tienen necesariamente porqué
seguir las leyes de las articulaciones reales, es posible añadir
operaciones de traslación y escalado (cambio de tamaño)
en cada articulación, llegando teóricamente a tener
nueve grados de libertad por cada una.
Desde el punto de vista de la informática
gráfica podemos imaginar la jerarquía articulada
como una estructura de datos que nos debe permitir dibujar las
partes del objeto en la posición adecuada. El algoritmo
que dibujara la escena debería recorrer recursivamente
la estructura articulada transformando el sistema de coordenadas
utilizado para la representación de los objetos. Si suponemos
que la representación visual de cada segmento rígido
está definida respecto a un sistema de coordenadas centrado
en el punto de articulación, entonces cada vez que el algoritmo
de recorrido llega a una articulación de la jerarquía
debe:
1.- Trasladar el sistema de coordenadas desde su posición anterior hasta el punto donde se conectará el siguiente segmento.
2.- Una vez trasladado allí, girar el sistema
de coordenadas según el estado de la articulación,
es decir, según los valores de los ángulos.
Si consideramos que cada articulación viene
definida por tres grados de libertad de rotación, entonces
son necesarios 3*n valores (n es el número
de articulaciones) para especificar completamente la posición
de la figura articulada. El conjunto de estos 3*n ángulos
se llama vector de configuración (
).
5.4.2. CONTROL DE LA JERARQUÍA
El problema que plantean los objetos articulados es el gran número de grados de libertad que poseen, un conjunto de números cuyo cambio en el tiempo debe especificarse para realizar la animación. Vamos a ver cuáles son los métodos de que disponemos para conseguir situar a la figura en las posiciones deseadas.
La dos formas de especificar la posición son
dar el vector de configuración
(los
ángulos de las articulaciones), o bien dar directamente
la posición final de cada segmento rígido, datos
que recogeremos dentro de un vector 
.
Hay dos variantes básicas para hacer el control de posición
con el tiempo:
En los métodos directos, dados los valores
de 
calcularemos los de 
.
En los métodos inversos, dado 
calcularemos 
.
Ambos tipos de métodos pueden combinarse con
keyframes de dos maneras diferentes: por un lado los keyframes
pueden describir la variación con el tiempo de los datos
iniciales (ángulos en el caso directo y las posiciones
en el caso inverso); por otro lado, una vez calculado el resultado
para ciertas posiciones de tiempo, estos valores pueden almacenarse
en forma de keyframes. De esta última forma, cuando la
animación deba ejecutarse de nuevo no será necesario
calcular otra vez el movimiento de la estructura articulada, sino
que se puede interpolar sobre los keyframes precalculados. En
este caso hay que evitar que los keyframes se encuentren excesivamente
separados en el tiempo, ya que la interpolación podría
producir resultados irreales.
Es el método más sencillo. Se calcula
mediante un mero cálculo geométrico,
sin tener en cuenta las propiedades dinámicas de la jerarquía
articulada (inercia, resistencia, peso). Este método es
muy eficiente, puesto que a partir de los ángulos de las
articulaciones podemos asignar fácilmente posiciones a
los segmentos recorriendo la estructura arbórea de forma
recursiva tal como hemos visto antes.
El inconveniente de este método es que no
facilita la colocación de la figura en la postura deseada
cuando existen muchos grados de libertad. Se emplea principalmente
para describir movimientos que no están orientados a objetivos,
sino que se desarrollan de forma mecánica y autónoma.
Al no considerar las variables dinámicas,
la cinemática directa puede producir efectos irreales desde
el punto de vista físico (por ejemplo, cambios instantáneos,
sin inercia ni aparente esfuerzo en el movimiento de un brazo
articulado largo). Por esta razón es conveniente hacer
el cálculo directo utilizando ecuaciones diferenciales
en las que aparezcan las fuerzas, momentos, torsiones, etc., aunque
esto significa aumentar considerablemente el coste computacional.
Los métodos inversos en los que se pretende
llegar a una relación 
conllevan
un proceso de cálculo mucho más costoso que los
directos, y por tanto resultan de difícil aplicación
para tiempo real (existen algunas aproximaciones de tipo iterativo
que pueden utilizarse), sobre todo cuando el número de
grados de libertad es elevado. Sin embargo este tipo de métodos
resultan casi imprescindibles para crear animaciones realistas
de figuras articuladas cuyo comportamiento está orientado
a objetivos, es decir, que tratan de alcanzar ciertas posiciones
(como coger un objeto con una extremidad o caminar sobre una superficie).
Uno de los inconvenientes de los métodos inversos,
y en particular de la cinemática inversa, es que pueden
existir infinitas soluciones para los valores de los ángulos
que llevan a una posición final dada, y debe elegirse solamente
una de ellas. También es posible que, debido a las restricciones
de la estructura (por ejemplo, no puede intersectarse consigo
misma), no exista solución.
Este último método, aunque el más
costoso, presenta una serie de ventajas frente a los descritos
anteriormente. Por un lado la introducción de criterios
dinámicos, principalmente el criterio de utilizar la mínima
energía posible en el desplazamiento, permiten reducir
el espacio de posibles soluciones para encontrar la óptima.
Además producen resultados muy naturales, puesto que las
estructuras articuladas naturales como las de los animales siguen
el mismo principio de mínima energía.
5.4.2.5 OTROS MÉTODOS COMPLEMENTARIOS
DE CONTROL
Hasta ahora hemos supuesto que el nodo raíz
de la jerarquía articulada era siempre el mismo. Resulta
evidente que la posición del segmento rígido que
actúa como raíz de la jerarquía no va a cambiar
en el proceso recursivo de evaluación, ya que éste
comienza precisamente a partir de ese nodo del árbol. Por
tanto, la posición del segmento raíz en el espacio
puede ser asignada de forma independiente y nos sirve para mover
la totalidad de la figura articulada por el espacio.
Sin embargo, hay ocasiones en que nos interesaría
poder determinar directamente la posición de otro segmento
de la jerarquía y, posiblemente, mantenerlo fijo. Por ejemplo,
cuando andamos mantenemos en contacto con el suelo uno de los
pies mientras nos desplazamos y luego cambiamos al otro pie. Podemos
en ese caso cambiar sobre la marcha el nodo raíz de un
pie a otro y reordenar la jerarquía cada vez, teniendo
en cuenta que las transformaciones realizadas en cada articulación
se invertirán.
Una condición adicional que deberíamos
utilizar para crear posturas estáticas y movimientos de
"balanceo" realista es asegurarlos de que el centro
de masa de toda la figura articulada cae sobre la vertical de
la superficie de sustentación (por ejemplo la formada por
la planta de un pie en el caso de sostenerse sobre uno solo, o
la que uniría los dos pies en el caso de apoyarse sobre
ambos).
Podemos combinar la estructura articulada, con especial
facilidad en el caso de la evaluación directa, con restricciones
basadas en funciones de transferencia como las que hemos comentado
antes. De esta manera disminuimos el número de grados de
libertad y resulta más fácil conseguir movimientos
en los que diferentes partes de la estructura están coordinadas.
Por ejemplo, podemos conseguir que los dos brazos de una figura
humana se muevan a la vez ligando sus ángulos con funciones
de transferencia que los igualan.
Hasta ahora hemos supuesto que los objetos no cambiaban
de forma con el tiempo, pero eso no siempre se corresponde con
la realidad. En muchos casos puede resultar interesante describir
estos cambios de forma, bien para introducirlos en la animación
o bien como una ayuda para modelar los objetos durante el proceso
previo de edición hasta que adopten la forma que nos interesa.
Veremos primero como introducción las técnicas utilizadas
para manipular imágenes y luego las extenderemos a los
objetos tridimensionales.
Recientemente se han popularizado en publicidad y efectos especiales cinematográficos las técnicas llamadas de morphing. Debemos distinguir claramente entre aquellos efectos que se basan en la manipulación de imágenes planas de aquellos otros que trabajan con una representación tridimensional. En el morphing de imágenes se utilizan dos efectos básicos; la deformación de la imagen, redistribuyendo sus colores y formas, y el fundido de dos imágenes, pasando de forma continúa de una a otra mientras la forma de los objetos parece interpolarse entre una y otra.
Ambos efectos parten de una descomposición
del espacio de la imagen en una malla de triángulos.
Para especificar un cambio continuo en la imagen basta con describir
cómo varía la posición de los vértices
de un instante de tiempo al instante posterior.
La clave para que la imagen se deforme de manera
coherente con la malla de triángulos es conseguir que para
cada triángulo original, el trozo de imagen que queda en
su interior se redistribuya sobre el mismo triángulo cuando
éste se transforma. Esto resulta muy fácil de implementar
representando la imagen como una textura bidimensionales sobre
una malla plana de triángulos (el uso de texturas se describirá
en el tema 7). El morphing se produce automáticamente cuando
se mueven los vértices pero no se alteran sus coordenadas
de textura originales. Si lo que se desea es hacer más
grande una parte del objeto, representado en la imagen se deberán
'estirar' los triángulos que lo cubren; si lo que se quiere
es hacerla más pequeña habrá que juntarlos.
Se puede también unir vértices de la imagen original,
con lo que ciertos triángulos desaparecerán completamente.
Para conseguir efectos interesantes de morphing es
necesario utilizar la malla de triángulos para efectuar
una partición de la imagen de forma que cada rasgo relevante
quede cubierto de manera más o menos precisa. Por ejemplo,
si queremos manipular la forma de una nariz en la imagen de una
cabeza humana, tendremos que recubrir la nariz con triángulos
marcando la frontera de los rasgos claramente.
La forma clásica (como se hace en cine o video)
para realizar un fundido entre dos imágenes es interpolarlas
en el tiempo, dando progresivamente más peso a una de las
imágenes y menos a la otra. Pero este sistema no realiza
una interpolación de las formas de los objetos que contengan
las imágenes inicial y final. Podemos utilizar el morphing
2D para ir distorsionando las dos imágenes al mismo tiempo
que fundimos la información de color. Para ello tenemos
que definir mallas triangulares en ambas imágenes y establecer
una correspondencia entre los vértices. Lo más sencillo
es buscar una correspondencia estructural, de manera que el vértice
correspondiente a un rasgo (por ejemplo, la punta de la nariz)
se corresponda en ambas imágenes, haciendo que éstas
isomorfas o coherentes. También es posible duplicar
o colapsar vértices durante el proceso.
En este caso no se trata de modificar una imagen
sino la forma de un objeto. Este cambio continuo puede utilizarse
en animación para representar deformaciones o crear efectos
visuales. Otro uso, más técnico, consiste en suavizar
las transiciones entre diferentes representaciones de un mismo
objeto cuando estas tienen diferente nivel de detalle (las técnicas
de nivel de detalle las presentaremos en el tema 6).
Aunque existen técnicas de morphing para otros
tipos de representaciones, la manera más común de
hacerlo es definiendo los objetos, al igual que en 2D, mediante
una malla de triángulos. La interpolación de la
posición entre la situación inicial y final se realizará
en este caso en el espacio tridimensional, y pueden también
interpolarse otras propiedades del objeto, como la textura o el
material.
Igual que en el caso bidimensional, las dos estructuras
de vértices pueden ser isomorfas, o también podemos
añadir o eliminar vértices. Esta última opción
se da cuando queremos efectuar la transición entre dos
niveles de detalle diferentes del mismo objeto, que están
caracterizados precisamente por tener un número diferente
de vértices.
Existen diferentes formas de añadir o quitar
vértices de forma continua. Una manera de hacerlo es acercar
(o separar) progresivamente los dos vértices. Debemos tener
en cuenta que cuando creemos nuevos vértices debemos reconstruir
la descomposición en triángulos de la superficie
(ver figura ***).
Recientemente esta técnica se ha extendido
para construir la llamada representación progresiva
de objetos poligonales, que permite el control continuo de nivel
de detalle. La representación progresiva de un objeto consiste
en una malla triangular básica, la de menor detalle, más
una lista de vértices que deben irse añadiendo para
pasar a versiones más detalladas del objeto (más
la información sobre su posición final de esos vértices).
5.5.3 CAMBIOS DE FORMA INDEPENDIENTES DE LA REPRESENTACIÓN
Las técnicas de morphing descritas tienen
dos problemas. El primero es que resulta costoso generar de forma
sencilla cambios globales en la forma del objeto (es más
útil para especificar cambios en los detalles). La segunda
desventaja es que se basan, salvo excepciones, en una representación
poligonal, y una vez descrito un cambio de forma, éste
es aplicable solo un cierto objeto, y en esa representación.
Vamos a ver ahora otras técnicas para describir cambios
de forma de forma matemática, y que por tanto pueden aplicarse
independientemente del sistema de representación y no dependen
de la forma concreta del objeto. Normalmente se utiliza para su
visualización un objeto geométrico sencillo (como
un cubo) que envuelve al objeto real, al que habrá que
aplicar la deformación según su posición
dentro de la figura envolvente.
Hemos visto que mediante la aplicación de
matrices a las coordenadas espaciales de los vértices de
un objeto es posible generar transformaciones del tamaño
y la posición del objeto llamadas transformaciones lineales.
Las tres transformaciones lineales más utilizadas son el
escalado, la traslación y la rotación. Sin embargo,
estas transformaciones lineales no alteran la forma básica
del objeto y (ésta es la razón de que se llamen
lineales) cada arista recta del objeto continúa siendo
recta después de la transformación.
La idea del método de Barr es utilizar estas
mismas transformaciones elementales, pero aplicándolas
de manera diferente a cada punto del objeto, dependiendo de sus
coordenadas. Como resultado, el efecto global de la operación
sobre la forma global del objeto es una transformación
no-lineal. Se suele utilizar como elemento básico envolvente
para visualizar el efecto de las operaciones un cubo.
Es posible escoger diferentes conjuntos de transformaciones
no lineales tomando unas u otras transformaciones básicas
y haciéndolas depender de las coordenadas x, y, z de diversas
maneras. Varios ejemplos de estas transformaciones globales podrían
ser:
Comprimir : se utiliza
el escalado de dos de las coordenadas en función de la
tercera; por ejemplo, el escalado para cada punto (x, y) variando
en función de z:
ESCALA x = f(z)
ESCALA y = f(z)
Retorcer : se aplica
una rotación a dos de las coordenadas que depende de un
ángulo que a su vez es función de la coordenada
restante.
Doblar : en este caso es la translación de dos de las coordenadas la que varía en función de una de la otra.
TRAS x, y = f(z)
Es una deformación basada en la especificación
de la transformación sobre un volumen paramétrico
como, por ejemplo, el hipertrozo tricúbico de Bèzier,
en el que cada lado es un trozo cúbico de Bèzier
definido por dos curvas cúbicas. O sea, cada arista viene
definida por cuatro puntos de control: los dos vértices
del cubo más dos puntos internos en la arista. En la posición
de reposo los puntos de control se encuentran en las caras de
un cubo.
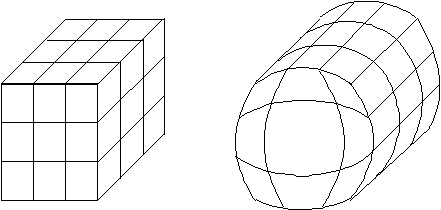
Cada vértice en el interior del cubo tiene
unas coordenadas paramétricas inducidas por la posición
de los puntos de control. Por tanto, para cada posición
de los puntos de control existe una relación:
El proceso de deformación funciona de la siguiente
forma:
5.5.4 ARTICULACIONES FLEXIBLES ( SKINNING
)
La representación visual de segmentos rígidos
en una figura articulada plantea el inconveniente de que la juntura
existente entre cada pareja de segmentos, no resulta natural,
sobre todo cuando intentamos representar cuerpos flexibles.
Para solucionarlo tenemos dos técnicas. La
primera se basa en un modelo de músculos que actúan
como formas elementales (usualmente elipsoides) para generar una
superficie equipotencial que represente el papel de 'piel', creando
una superficie contínua que da una mejor apariencia a la
articulación. La segunda técnica emplea volúmenes
paramétricos concatenados (hipertrozos como los que hemos
visto en el método FFD). Uno de estos hipertrozos estará
conectado a los dos segmentos rígidos (ver figura 5.5.4.)
y resultará deformado por el movimiento de la articulación.
Mediante el método FFD calcularemos la correspondiente
transformación suave de una superficie intermedia que representa
el tramo de la articulación.
