Una vez hemos estudiado las diferentes formas de
representar los objetos tridimensionales que van a formar parte
de la escena que deseamos visualizar, tenemos que analizar cómo
estos objetos responden a la luz, de manera que podamos figurarnos
cómo simular por ordenador ese proceso y dotar a los objetos
sintéticos de un aspecto realista en función de
las fuentes de luz, superficies y medios materiales que hayamos
definido.
2.1. CARACTERIZACIÓN DE LA LUZ.
Para caracterizar físicamente la luz nos interesará
la dirección en la que viajen los rayos (direccionalidad)
y la distribución de intensidad energética, magnitud
ésta que se relacionaría con la producción
de un determinado color cuando la luz alcanzara el ojo del observador
u otro tipo de detector.
En nuestro modelo utilizaremos ciertas aproximaciones
bastante comunes. Una de ellas será considerar que la luz
viaja en línea recta y atraviesa medios más o menos
homogéneos. En realidad, si el medio tuviera un índice
de refracción que variara de forma continua (fenómeno
que se produce, por ejemplo, en la atmósfera y en ciertas
lentes) la luz tendría una trayectoria curva. La luz también
puede curvarse debido a efectos de difracción (al pasar
por bordes o rendijas), y tal como explica la Teoría de
la Relatividad General, también cuando pasa cerca de masas
muy grandes. Pero estas situaciones son extraordinariamente raras,
en el sentido de que difícilmente somos capaces de percibirlas
en un entorno normal.
Otra aproximación inicial es considerar que
la información de fase resulta irrelevante para
nuestro modelo. La luz es una composición de ondas, que
además de caracterizarse por su frecuencia y su amplitud
(relacionada con la energía que transportan), también
tendrían una determinada fase según la posición
en la que se encuentran las 'crestas' y 'valles' de la onda respecto
a un origen arbitrario de distancias. El único fenómeno
perceptible que se debe a la fase, y que por tanto dejaríamos
de considerar en nuestro modelo, es el de la interferencia
de ondas de luz. En determinadas condiciones las crestas y valles
de varias ondas de luz que se combinan se hacen visibles, pero
de nuevo se trata de situación relativamente rara en los
entornos normales.
La intensidad luminosa nos definirá
la densidad de energía que transporta el rayo luminoso.
Podemos medirla en relación a diferentes magnitudes físicas,
por ejemplo respecto al tiempo 
, o a la
cantidad de superficie atravesada por la onda 
. Una de las definiciones que más se suele utilizar en
informática gráfica sentido es la llamada radiosidad
(B), la intensidad luminosa por unidad de tiempo y de superficie
perpendicular atravesada :
También se define otro tipo de intensidad,
la radiancia, donde se considera que la luz parte de un punto
y se divide la radiosidad por el ángulo sólido abarcado
por la onda luminosa desde el punto emisor 
[Esto lo veremos en detalle al estudiar ENLACE el modelo global
de comportamiento de la luz].
Para caracterizar energéticamente una fuente
de luz se emplea el espectro luminoso. La luz natural está
compuesta por distintas longitudes de onda , o visto de otro modo,
por gran diversidad de frecuencias o períodos de onda
T diferentes. Siendo c la velocidad de la luz, la
relación entre estas magnitudes es:
El espectro de una radiación se define, entonces,
como la función que nos da la intensidad de la radiación
en función de la frecuencia (o equivalentemente, de la
longitud de onda). El espectro luminoso (visible) está
constituido por aquel intervalo de frecuencias que puede detectar
el ojo humano y es solamente una parte dentro espectro total de
las radiaciones electromagnéticas (ver FIGURA ESPECTRO
con visible, ultiravioleta, etc.).
Ciertas características de la función
de intensidad están relacionadas con la sensación
cualitativa del color, y por tanto conviene analizarlas.
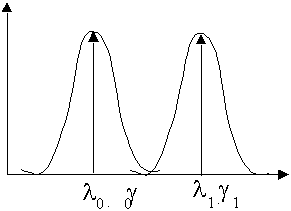
* Tono: desde el punto de vista de la visión
del color, el tono es lo que diferenciaría cualitativamente
los diferentes colores perceptibles, independientemente de su
brillo y su pureza. Físicamente podríamos definirlo
por medio de longitud de onda (o frecuencia) predominante en el
espectro de luz, es decir, por su punto de intensidad máxima.
* Saturación: desde el punto de vista
de la visión, equivale a la pureza del color. Se dice que
un color es más 'puro' cuanto más saturado esté.
Desde la perspectiva física, un espectro es más
saturado cuanto más monocromático sea, es decir,
cuanto más se parezca a una función de intensidad
que solamente sería diferente de cero para un valor único
de frecuencia. Como una luz blanca posee componentes en todas
las frecuencias del espectro, disminuir la saturación de
un color equivale a sumarle un cierto porcentaje de luz blanca.
* Luminosidad: desde el punto de vista de
la visión, se trata de lo brillante que es percibido el
color, independientemente de sus diferencias de tono y pureza.
Físicamente esta magnitud tiene que ver con la energía
total o intensidad total del espectro. Se trata, por tanto, de
la integral de toda el área cubierta por el espectro.
El ojo humano y de muchos animales está compuesto
por dos tipos fundamentales de detectores, que son los bastones
y los conos. Estos detectores responden a la energía luminosa
que les va llegando de diferentes partes del espectro. Los bastones
se utilizan en la visión nocturna y responden básicamente
a la luminosidad, por lo que no efectúa una distinción
entre los diferentes colores. Sin embargo, existen tres tipos
de conos que responden a diferentes colores del espectro, y que
por tanto se suelen denominar como detectores de radiación
Roja, Verde y Azul.
Para caracterizar un color podemos descomponer la función espectral en una combinación lineal de las funciones a las que son sensibles cada uno de estos detectores:
El espectro de la intensidad luminosa será:
.
Por ello, en la síntesis de imágenes 3D se suele caracterizar un color por medio de sus componentes R,V,A (Red, Green , Blue en inglés) y efectuar con ellas los cálculos de iluminación. Sin embargo, existen modelos más precisos que mantienen una discretización mucho más fina del espectro luminoso.
El proceso de generación de una imagen en
la pantalla del ordenador es de alguna manera inverso al de la
percepción, de modo que los puntos rojo, verde y azul de
una pantalla o proyector tendrán unos espectros de emisión
para una de las tres componentes que serán lo más
similares posibles al espectro detectado por cada tipo de sensor.
De esa forma, para reproducir un cierto color no tenemos más
que producir una excitación luminosa con los valores (R,V,A)
correspondientes en cada punto.
En realidad existen muchas restricciones en la manipulación
del color, y toda una teoría compleja que intenta dar cuenta
de ella. El sistema R, V, A es solamente un posible sistema de
representación en el que se efectúa una suma aditiva.
[ENLACE AL TEMA DE IG de segundo donde se explica color]
La luz sufre una serie de transformaciones tanto
en su espectro como en la direccionalidad de sus rayos cuando
interactúan con otros objetos. Debemos estudiar esas interacciones
para poder hacernos idea de cómo reproducirlas en el ordenador.
2.2.1. INTERACCIÓN CON UNA SUPERFICIE
Desde el punto de vista de la luz una superficie
activa es una zona que separa dos medios de diferente índice
de refracción. La interacción de una luz con una
superficie es la más comúnmente aplicada en gráficos
de síntesis. Consideraremos una fuente emisora de luz y
un punto en la superficie de cierto objeto. En general tenemos
como resultado que la distribución de intensidad incidente
será en parte absorbida por la superficie, en parte devuelta
al medio de donde provenía (componente reflejada) y en
parte pasará al segundo medio tras la superficie (componente
transmitida):
Donde :
Es común hacer la aproximación de que el comportamiento de la luz no tiene dependencia del ángulo i (comportamiento isótropo) pero en muchos materiales, como los tejidos, sabemos que la dirección de la luz incidente respecto a las fibras puede determinar la forma en que se produzca la reflexión (comportamiento no isótropo). A partir de ahora supondremos que todas las superficies son isótropas, tanto respecto a la intensidad reflejada como a la transmitida.
También efectuaremos a partir de ahora la
aproximación de caracterizar la distribución espectral
por medio de las tres componentes r,v,a o r,g,b, en lugar de tener
una representación continua de la intensidad. Por tanto,
cuando en una cierta fórmula escribamos acerca de la Intensidad,
nos estamos refiriendo a cada una de sus tres componentes de color,
cuyo comportamiento se caracterizaría por una ecuación
independiente.
Vamos a ver primero cómo efectuar aproximaciones
sencillas a las distribuciones reflejada y transmitida, para luego
combinar estas aproximaciones en un modelo local de iluminación.
2.2.2. APROXIMACIONES A LAS DISTRIBUCIONES REFLEJADA
Y TRANSMITIDA:
1.- Componente Ambiente.
Supondremos que sólo existe una dependencia
respecto a la intensidad de la fuente, despreciando todos los
otros factores:
Donde 
es el coeficiente
de reflexión o transmisión de luz ambiente,
que en realidad tendría un valor diferente para cada componente
de color: 
.
El comportamiento que representa esta ecuación
es muy simple: cuanto más luz emiten las fuentes, más
se ilumina la superficie, independientemente de cómo está
orientada, dónde esté el observador, etc. No tiene
en cuenta para nada la dirección, el color observado en
la superficie sería el mismo desde cualquier punto de vista.
La utilidad de esta componente reside en que sirve
para iluminar con un color constante aquellas partes de los objetos
que normalmente no recibirían luz directa, evitando así
las sombras demasiado oscuras.
2.- Componente Difusa.
( reflexión o transmisión
difusa ) .
En este caso tanto la distribución de intensidad
reflejada 
y transmitida 
son isótropas, iguales en todas las direcciones, no dependen
del punto de vista del observador, es decir, desde cualquier
punto se percibirá la misma intensidad, y por tanto el
mismo color aparente, en la superficie. Pero al contrario que
en el caso de la componente ambiente, ahora esta intensidad reflejada
o transmitida sí dependerá de dónde coloquemos
la fuente emisora de luz respecto a la superficie. En concreto,
dependerá del coseno del ángulo de incidencia
de la luz, el formado por la dirección de la luz incidente
con el vector normal de la superficie. Esta ecuación se
conoce también como ley de Lambert.
Con un modelo de comportamiento difuso se podría
realizar ya realizar un sombreado más o menos realista
de un objeto aislado, consiguiendo darle la apariencia de volumen.
Debemos tener en cuenta, sin embargo, que el comportamiento difuso
es una aproximación, y solamente materiales rugosos o porosos
muy homogéneos, que no reflejan la luz en ninguna dirección
privilegiada, se comportan de forma casi difusa. Por otro lado,
los medios transmisores de la luz con comportamiento únicamente
difuso también son raros. Se trataría de materiales
que actúan como filtros difusores, del tipo de los utilizados
en luminotecnia para eliminar las sombras de una escena añadiendo
iluminación difusa.
3.- Componente Especular.
Es muy normal que la intensidad reflejada o transmitida
lo haga predominantemente en una dirección que viene dada
por la ley de reflexión o de refracción (para la
componente transmitida):
Pero, al contrario de lo que supone la óptica
geométrica, el comportamiento especular nunca es perfecto:
no todos los rayos salen en la misma dirección, sino que
se tiene una cierta dispersión (anchura de la distribución
especular). Según lo separado que esté el observador
de la dirección de mayor intensidad (esta separación
la mide el ángulo 
), percibirá
más o menos intensidad. Tendremos que:
donde 
es un factor que mide
el decrecimiento de la intensidad alrededor de la dirección
principal. El parámetro s (shininess o brillo)
controla lo rápido que es este decrecimiento, de manera
que cuando mayor sea s, más apuntada es la función
y por ello más 'perfecto' es el
comportamiento especular.
Aproximando 
por una constante
2.2.3. MODELOS DE SOMBREADO LOCAL.
A la hora de realizar la iluminación (asignación de colores) de una escena podemos optar por el empleo de un modelo local o global. En este apartado vamos a centrarnos en las características de los modelos locales, que son más sencillos de implementar y menos costosos computacionalmente.
En un modelo local, para calcular la intensidad que percibimos (el color) procedente de un cierto punto de una superficie, se tiene en cuenta la posición de ese punto en el espacio, el vector normal a la superficie en el punto, la posición de las fuentes de luz, las características que definen el material y la posición del observador (en el caso de considerar la componente especular).
En los métodos locales no se consideran las
interacciones entre los objetos y por ello no nos permiten crear
sombras ni reproducir la influencia de la luz reflejada o transmitida
por un objeto sobre los otros cuerpos de la escena. Es como si
a la hora de calcular la iluminación de un objeto los demás
desaparecieran de la escena, lo que hace el proceso más
rápido y eficiente. El coste de la iluminación sería
lineal con el número de puntos a iluminar y el número
de fuentes de luz, además de depender de otros factores.
Es por ello que, como veremos, se usa para la producción
de gráficos en tiempo real [ENLACE].
Los modelos de sombreado local combinan todas las
aproximaciones que hemos visto anteriormente y añaden otros
efectos como la emisión propia de luz por parte de la superficie.
Las características del material que forma la superficie
de los objetos vienen determinadas por una serie de coeficientes
, cada uno de los cuales tendrá
tres versiones para cada componente de color (r, g, b). Por ejemplo,
para caracterizar la distribución de intensidad reflejada
tendríamos:
De donde se obtiene la ecuación que engloba
todas las componentes:
Podemos simplificar esta ecuación considerando
que no existe atenuación de la fuente, es decir, que 
Este es el modelo básico de sombreado. Para
calcular los colores a partir de los valores de intensidad habrá
que tener en cuenta los límites en el rango de las componentes
de color. Los valores de los coeficientes se suelen definir entre
0 y 1. Si suponemos que cada componente 
,
se debe normalizar la fórmula de manera que el valor resultante
para cada componente de 
nunca sea mayor
que uno cuando las intensidades incidentes también se limitan
a este intervalo.
2.2.4. OTROS EFECTOS SOBRE LA LUZ
2.2.4.1 ATENUACIÓN CON LA DISTANCIA
Al ser una onda física que se va expandiendo
por el espacio, la intensidad local de la luz se atenúa
con la distancia. Puesto que la misma energía, emitida
desde un cierto punto, se distribuye en un espacio esférico
cuya superficie aumenta con el cuadrado de la distancia, llegamos
a la conclusión de que la intensidad a una distancia d
de la fuente será proporcional al inverso del cuadrado
de d: 
. Para una fuente que consideramos
a una distancia infinita [ENLACE a TIPOS FUENTES]., como por ejemplo
el Sol, supondremos que no existe atenuación. Pero si intentamos
aplicar esta aproximación de la atenuación con el
inverso del cuadrado en nuestros modelos de sombreado local obtendremos
atenuaciones demasiado bruscas para las fuentes de luz que no
están en el infinito La razón es que en un entorno
real la luz de una fuente local se distribuye por la escena y
llega luego a los objetos desde diferentes puntos por efecto de
la interdifusión, haciendo que el efecto global de la atenuación
con la distancia no sea tan brusco.
Por esta razón en gráficos de síntesis
se suele utilizar una función polinomial más general,
donde podremos controlar la suavidad de manera que la atenuación
de la luz no varíe bruscamente.
2.2.4.2. ATENUACIÓN POR ABSORCIÓN
(FILTRADO)
Cuando la luz atraviesa un medio físico (sólido,
líquido, gas) y recorre una cierta distancia, se produce
una atenuación debida a la absorción del medio de
parte de la intensidad luminosa. Este fenómeno no solamente
causa una disminución de la intensidad total, sino que
al producirse una absorción diferente para cada componente
de color, también se altera el equilibrio general de color.
Si suponemos que el medio es homogéneo y viene
caracterizado por una constante de absorción k,
para representar el efecto de la absorción con la distancia
r se debería emplear una función de decrecimiento
exponencial 
.
De este modo se trata de simular lo que ocurre en
la realidad pero en la práctica no funciona tan bien como
cabría esperar ya que esta atenuación produce unos
efectos muy bruscos. Es por ello que se suele usar un modelo de
decrecimiento lineal 
.
Veamos unos ejemplos prácticos donde se podría
utilizar estos efectos:
- Trazado de rayos para iluminar una esmeralda.
El color que observamos se debe a que parte de la
luz que incide por la superficie es absorbida y parte reflejada.
Para el caso de la esmeralda la coloración verdosa aparece
porque la absorción de la componente verde de la luz no
sería tan grande como para las componentes roja y azul.
- Simulación de efectos atmosféricos:
Como hemos indicado anteriormente el hecho de producir una absorción totalmente homogénea no es realista, además de producir efectos no deseados como cambios bruscos de luz. Por ejemplo en la atmósfera la absorción de la luz solar dependerá de la cantidad de microgotas que existiesen en ella. En la niebla real tendremos que la constante k será una función variable, y por tanto tendríamos que realizar el cálculo de una integral a lo largo del recorrido del rayo. Otra complicación es que en el efecto de la niebla influye no solamente la absorción de la luz que proviene del objeto, sino también la difusión de la luz proveniente del Sol y otros objetos, aspecto que veremos en el siguiente apartado.
Este efecto es diferente al de la esmeralda. En
la esmeralda si su absorción es muy brusca el objeto se
vuelve negro. En la niebla influye la luz solar, esta luz se va
difundiendo en todas las direcciones y por tanto hay que tener
en cuenta.
2.2.4.3. MODIFICACIÓN POR DIFUSIÓN:
Otro fenómeno que sufre la luz al pasar por
un medio es el de la difusión. Por un lado parte de la
intensidad se desvía al interaccionar con las partículas
del medio. No es que la energía sea absorbida, sino que
es reenviada en otra dirección. Un ejemplo de este primer
efecto de la difusión es la coloración de la atmósfera
debida a la luz del Sol. La componente azul de la luz solar se
difunde más que la verde y la roja, y ésta es la
razón de que el Sol tienda a aparecernos amarillo-anaranjado,
especialmente cuando está bajo sobre el horizonte y su
luz atraviesa la atmósfera a lo largo de una distancia
mayor.
Por otro lado la luz que ha sido desviada de su curso
original (por ejemplo, proviniente del Sol) puede llegar al observador
como si viniera aparentemente desde otro sitio, dando una coloración
a esa parte de la escena que no se debe a los objetos que contiene.
Así, la luz azul que es difundida por la atmósfera
desde el Sol es la que le otorga su tonalidad característica
al fondo celeste. La niebla difunde la luz solar y hace que parte
de ella vaya hacia el observador, por lo que los objetos lejanos
se funden en el color blanquecino y pierden el suyo propio, es
decir, se dan al mismo tiempo dos efectos: la disminución
del color propio del objeto debida a la absorción de la
niebla y la adición de un color blanco debido a la difusión
de la luz solar.
2.2.5. TIPOS DE FUENTES DE LUZ
A la hora de calcular la iluminación deberemos también considerar cómo es generada la intensidad de luz que luego incidirá en los objetos. Podemos clasificar las fuentes de luz como:
* Direccionales: emiten rayos paralelos, como
si estuvieran localizadas en el infinito. No poseen atenuación
debida a la distancia.
* Puntuales: se trata de fuentes localizadas
en ciertas coordenadas no infinitas (fuentes locales), que emiten
por igual en todas las direcciones.
* Puntuales direccionales (focos):
también son locales, pero emiten preferentemente en una
dirección determinada..
* Fuentes extensas: se trata de una fuente,
local o en el infinito, que emite desde más de un punto
(si es local) o dirección (si es infinita). El tratamiento
de una fuenta de este tipo siempre va a involucrar un cierto proceso
de integración, sea analítica o descomponiendo la
fuente en elementos de comportamiento conocido, como puntos o
polígonos. Existen ciertos métodos, como la radiosidad,
que permiten trabajar directamente con fuentes extensas [ENLACE].
A diferencia de las fuentes puntuales, éstas producen una
zona de penumbra en los bordes de las sombras.
2.3. COLORACIÓN DE LOS OBJETOS
Para colorear el objeto lo que debemos hacer es asignar
componentes de color RGB a todos sus puntos visibles, es decir,
a aquellos que resultan proyectados en nuestra ventana de visión.
Existen dos métodos básicos para evaluar el color
de estos puntos. Uno consiste en hacerlo directamente enviando
un rayo en esa dirección y calculando la intensidad de
luz que transportará hacia el observador [ENLACE TRAZADO
RAYOS]. El otro método consiste en evaluar el color solamente
para ciertos puntos, normalmente los vértices de una descomposición
poligonal del objeto (ver [ENLACE A VISUAL. TIEMPO REAL]), para
luego interpolar el color de los puntos intermedios. Vamos a analizar
ahora esta segunda forma de cálculo.
Supondremos que nuestro objeto se ha descompuesto
en polígonos, y éstos a su vez en triángulos.
De cada vértice conocemos su posición y su vector
normal. Si los tres vectores normales de los vértices del
triángulo coinciden, es decir, consideramos que el triángulo
debe iluminarse como si fuera efectivamente plano (una faceta),
entonces todo el polígono se colorea de un mismo tono (sombreado
plano o por facetas). Sin embargo, si las normales son diferentes
tenemos que hacer variar el color en el interior del triángulo
mediante una interpolación. Hay dos métodos básicos
de realizar esta interpolación, los de Gouraud y
Phong.
2.3.1. MÉTODO DE GOURAUD (Interpolación lineal del color).
En este caso se calcula el color de cada vértice
utilizando las propiedades materiales y la dirección del
vector normal. El cálculo del color de cada punto interno
del triángulo se realizará como una interpolación
lineal entre los colores de los vértices. Si representáramos
en el espacio las dos coordenadas x,y de cada vértice y
el color como una tercera coordenada, podríamos calcular
el color de los puntos internos del triángulo como aquellos
correspondientes al plano que pasa por los tres vértices
[DIBUJO].
La forma eficiente de realizar esta interpolación
es utilizar un algoritmo de rellenado incremental [ENLACE A TIEMPO
REAL, donde se explique el algoritmo de rellenado].
2.3.2. MÉTODO DE PHONG (INTERPOLACIÓN
DE LAS NORMALES).
El método de Gouraud es muy rápido,
pero produce efectos visuales poco realista. Si los polígonos
aparecen muy grandes en la ventana de visualización, se
apreciarán cambios no suaves en la coloración, observándose
las fronteras entre triángulos. El método de Phong
consiste básicamente en calcular el valor del vector normal
para cada punto interno del triángulo y aplicar entonces
el modelo de iluminación para calcular el color en ese
punto.
El coste de este método es más elevado,
puesto que las operaciones involucradas en el modelo de iluminación
son más costosas que meras sumas y multiplicaciones. Sin
embargo, el resultado es mucho más realista. Se suele utilizar
al efectuar el trazado de rayos de objetos descritos por primitivas
poligonales.