Existen varias razones para querer representar un
objeto mediante un modelo de superficie:
En cualquiera de estos casos es conveniente utilizar
una representación de la superficie del objeto. En principio
la información sobre una superficie debe dar cuenta de
su geometría, de sus propiedades visuales (cómo
se comporta frente a la luz [LINK A MODELO LUZ-SUPERFICIE]) y
quizás también de alguna propiedad física
(como la elasticidad) si se va a efectuar una simulación
física sobre el objeto.
Si la totalidad del objeto consta de diferentes partes
(por ejemplo, varios polígonos o varios trozos definidos
por diferentes ecuaciones), entonces podemos añadir también
información topológica, es decir, sobre cómo
estas diferentes partes se conectan entre sí para formar
la superficie. Con esta información adicional el modelo
se conoce como una representación de frontera del
objeto (b-rep: boundary representation). Esta representación
de frontera se utiliza frecuentemente en combinación con
un modelo sólido, ya que una de ellas se puede reconstruir
a partir de la otra.
En general, las diferentes representaciones no se
excluyen entre sí, y muchos programas suelen combinarlas,
pasando de una a otra según convenga.
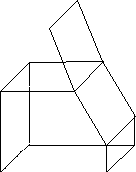
Una característica que suele exigirse a las
superficies representadas es que sean variedades bidimensionales
(en inglés: superficies 2-manifold), es decir, que
no existan puntos singulares donde la superficie se intersecte
consigo misma o se abra en varias hojas. Ver figura 1.1

Consiste en definir el objeto a través de
una superficie formada por polígonos que comparten sus
aristas y vértices, es decir, de un poliedro, que puede
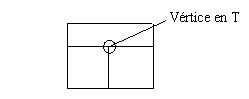
ser abierto o cerrado. La exigencia de que sea una variedad bidimensional
se traduce, en este caso, en la restricción de que los
polígonos no se intersecten entre sí excepto en
las aristas, y que en una arista no puedan confluir más
de dos polígonos. En un vértice pueden coincidir
cualquier número de polígonos.
Además, una buena representación poligonal
debe tener en cuenta:
La representación basada en polígonos
tiene la ventaja de que permite hacer una visualización
muy rápida, porque únicamente se deben realizar
una serie de operaciones lineales muy eficientes, tanto para la
proyección sobre la pantalla como para el posterior rellenado
de los polígonos, gracias a lo cual es muy adecuada para
representaciones en tiempo real [ENLACE]. Como veremos después,
su visualización mediante trazado de rayos, en concreto
el cálculo de intersecciones [ENLACE] también resulta
especialmente simple.
Sin embargo, los objetos complejos o de origen natural
raras veces están descritos perfectamente por medio de
polígonos exactos, por lo que en su representación
por este método se deberán realizar aproximaciones
, haciendo que la superficie aparezca formada por 'trozos' no
suaves claramente visibles.
[AÑADIR AQUÍ ECUACION DEL PLANO Y LA FORMA DE UTILIZARLA PARA DISTINGUIR INTERIOR/EXTERIOR EN OBJETOS CONVEXOS]
".ENLACE A CARACTERÍSTICAS DE LOS POLÍGONOS."
1.1.1.1. REPRESENTACIÓN POR POLÍGONOS AISLADOS
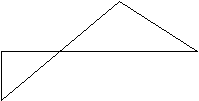
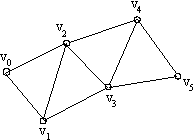
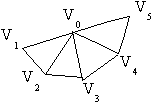
En este caso un poliedro se representa mediante una
lista de polígonos, siendo cada uno de éstos una
lista de vértices o de aristas. Hay que tener cuidado a
la hora de definir polígonos con más de tres puntos,
ya que cuatro puntos no tienen porqué ser coplanarios en
el espacio de tres dimensiones y al proyectarlos para formar una
imagen bidimensional, los resultados pueden no estar bien definidos
(ver un ejemplo en la figura 1.1.1.1.A).
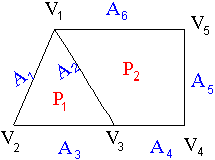
Para ello poder incorporar información topológica,
de relación de vecindad entre los polígonos, hay
que construir una estructura de datos en la que se especifiquen
las referencias adecuadas.
Vamos a ver un par de formas de representar un conjunto de polígonos en forma de tabla, de manera que sea posible extraer información topológica. La primera forma contendría:
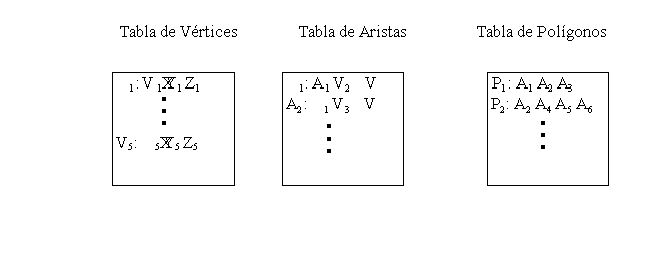
De forma que será muy sencillo comprobar si
dos polígonos se tocan pues deberán compartir al
menos una arista.
O bien :
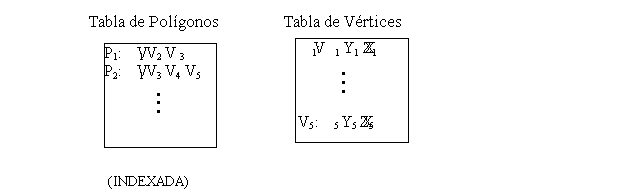
Estas representaciones se pueden reducir eliminando
información redundante, o añadir más información
para facilitar la búsqueda de relaciones entre los diferentes
elementos. Aparece por tanto, la necesidad de un compromiso entre
la cantidad de almacenamiento requerida, la complejidad de la
estructura de datos y la rapidez de acceso a la información
geométrica y topológica.
Un mismo vértice puede formar parte de diferentes
polígonos. Si guardamos la información de cada vértice
(posición, vector normal, color, etc.) una sola vez y luego,
cuando describamos los polígonos de los que forma parte,
hacemos referencia a él mediante su índice en la
tabla de vértices entonces se dice que estamos describiendo
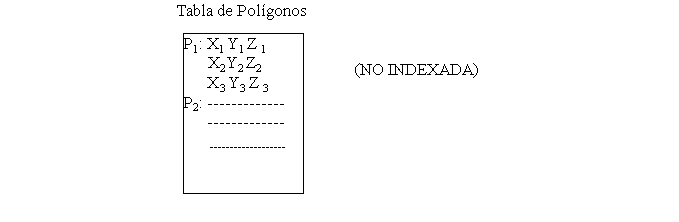
el objeto de forma indexada. Si, por el contrario, cada
vez que un vértice aparece en la descripción de
algún polígono repetimos toda la información
correspondiente al vértice, entonces estamos trabajando
con una estructura no indexada.
La estructura indexada tiene la ventaja de ahorrar
espacio de almacenamiento. Sus desventajas son que no permite
la discontinuidad de color u otra magnitud asociada a los vértices,
ya que dos polígonos que comparten el mismo vértice
tienen la misma normal en ese punto. Esto produce un efecto de
suavizado del color de la superficie que a veces resulta irreal
(ver Figura 1.1.1.1.B). Otra desventaja es que se produce un ligero
aumento en el tiempo necesario para una consulta de datos sobre
los vértices, ya que primero debe averiguarse el índice
y luego buscar la información deseada en la tabla.
En caso de emplear una lista no indexada, se puede
representar un poliedro con una única lista de polígonos,
definidos por las coordenadas de cada uno de los vértices
que lo componen. Al no disponer de una tabla de vértices,
se consigue acceder de forma mucho más rápida a
las coordenadas, puesto que ahora se obtienen con un único
acceso. Sin embargo, tiene el inconveniente de aumentar considerablemente
el espacio de almacenamiento necesario, ya que las coordenadas
de los vértices aparecen repetidas cada vez que un mismo
vértice pertenece a varios polígonos distintos.
1.1.1.2. MALLAS POLIGONALES ( PRIMITIVAS POLIGONALES
)
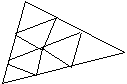
Las primitivas o mallas poligonales son grupos de
polígonos que se describen de forma conjunta para ahorrar
espacio de almacenamiento y coste de visualización en tiempo
real, razón por la cual son ampliamente utilizadas.
Algunas de las primitivas más utilizadas son:


En realidad, la mayor parte de aplicaciones y librerías
gráficas descomponen posteriormente todas estas primitivas
en triángulos durante el proceso de visualización.
La ventaja de las representaciones poliédricas
es que son más adecuadas para la visualización utilizando
el hardware gráfico que trabaja con polígonos. El
problema que plantean es que la mayoría de los objetos
no son realmente poliedros, sino que están compuestos por
superficies contínuas curvadas.
Para representar un objeto complejo se puede utilizar
una descomposición de la superficie en trozos o parches
(patches) triangulares o cuadrangulares, cada uno de los
cuales se suele modelar con superficies paramétricas (superficies
de Bezier, NURBS...). Estas superficies proporcionan, como veremos
luego, una mayor facilidad para el modelado, ya que en el caso
de tener una descripción que contenga muchos polígonos
resulta tedioso modificar la posición de cada uno de los
vértices para ir cambiando la forma del objeto. Si despues
de la fase de modelado utilizando superficies curvas es necesario
hacer una visualización en tiempo real, entonces puede
efectuarse una descomposición poligonal de la superficie
suave (del nivel de detalle que nos convenga).
Los problemas que plantean con este tipo de representación
contínua a trozos son, por una parte, la dificultad de
controlar que la forma de la superficie es exactamente la que
queremos y por otro la complejidad de mantener las restricciones
(continuidad, derivabilidad) en las intersecciones de los trozos.
Para definir una superficie curvada y suave de forma
exacta debemos recurrir a una representación analítica,
es decir, mediante ecuaciones. Dependiendo de la forma de las
ecuaciones habrá que evaluar la superficie (hallar sus
puntos) utilizando distintos métodos. En general tenemos
los siguientes tipos:
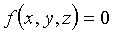
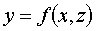
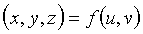
En tres dimensiones una ecuación explícita siempre puede transformarse en paramétrica, como podemos ver en el siguiente ejemplo:
Si 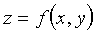
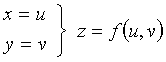
1.1.2.1. SUPERFICIES PARAMÉTRICAS : SUPERFICIES
DE CONTROL.
Vamos a examinar alguna de las formas de proceder
con una superficie paramétrica, que mostrarán lo
simple que resulta su utilización en ciertos algoritmos
y su visualización. Si se emplean las ecuaciones paramétricas
para definir una superficie, es posible hallar puntos que pertenezcan
a ella (por ejemplo, para poder dibujarla) sin más que
ir dando valores a los parámetros u y v,
de tal forma que se recorre la superficie de forma exhaustiva.
En muchas representaciones se normaliza la ecuación de
manera que los parámetros u y v solamente
tomen valores en el rango [0,1].
Además se pueden calcular muy fácilmente
algunos parámetros interesantes, como pueden ser :
El problema de esta aproximación es que la
complejidad de las ecuaciones suele aumentar enormemente cuando
imponemos muchas restricciones (por ejemplo, que la superficie
pase por más y más puntos que nos interesan). También
aparecen efectos indeseados; las superficies resultantes pueden
tener una forma extraña aunque pasen por los puntos como
puede verse en el siguiente dibujo.
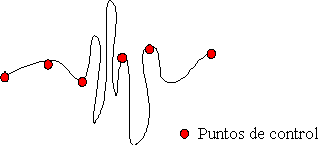
Al aparecer ordenadores capaces de representar gráficos,
y comenzar su aplicación en el Diseño Asistido por
Ordenador (CAD), surgieron grupos de investigación en empresas
de automóviles que desarrollaron la teoría y la
aplicación de ciertas superficies paramétricas cuya
forma se podía definir de manera sencilla a través
de puntos de control, garantizándose que su forma
no sufra variaciones incontrolables. Las curvas más interesantes
son construidas a partir de polinomios y cumplen con la siguiente
propiedad: si definimos el cierre convexo de un conjunto
de puntos como el mínimo polígono convexo (en 2D)
o poliedro convexo (en 3D) que los contiene, entonces se cumple
que la curva o superficie determinada por un conjunto de puntos
de control no se sale del cierre convexo de estos puntos.
No vamos a especificar aquí en detalle los
diferentes tipos de superficies paramétricas polinómicas
con puntos de control. Las más empleadas son las "s_bezier.htm"[ENLACE]
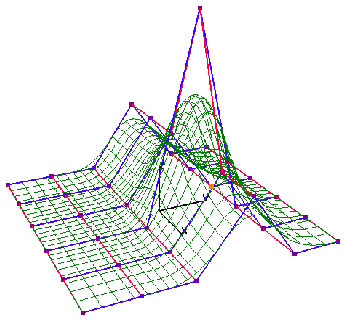
superficies de Bèzier, las B_Splines y las NURBS (ver Figura
1.1.2.1.). Su forma general sería:
ECUACION GENERAL: X(u,v) = …[ENLACE Sup. Bèzier)

Para realizar la visualización de estas
superficies primero habrá que evaluar los polinomios que
aparecen en su expresión analítica. Ya hemos visto
que una forma de dibujar la superficie sería ir dando valores
a los parámetros u y v. Para acelerar la evaluación
de los polinomios podemos utilizar el método de Horner
, ya que para un polinomio de grado N solamente utiliza N multiplicaciones
y N sumas: [EJEMPLO].[ENLACE Horner]
Otras formas de optimizar estos cálculos se
basan en el calculo de incrementos a partir de un primer punto
"incre_dif.htm" [ENLACE cálculo de incrementos
diferenciales] o en la realización de sucesivas subdivisiones
de forma adaptativa "subdi.htm" [ENLACE Métodos
de subdivisión].
1.1.2.2. SUPERFICIES IMPLÍCITAS : ISOSUPERFICIES
Y SUPERFICIES EQUIPOTENCIALES.
Otro método de modelado especial de superficies consiste en definirlas como funciones en forma implícita, es decir, en la forma F(x,y,z)=0 y luego buscar alguna manera de visualizarlas. Esto es equivalente a definir un campo escalar en el espacio y luego tomar todos los puntos x,y,z en los que esa magnitud toma un valor constante.
De esta forma, a partir de una función 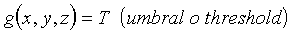
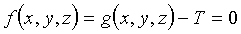
Este tipo de objeto se denomina también isosuperficie.
Si el campo escalar varía de forma suave (existe su gradiente
o derivada respecto a la posición) entonces se denomina
potencial (como el generado por un campo de fuerza en física).
En ese caso la isosuperficie se denomina superficie equipotencial.
Una forma de poder controlar la forma de esas superficies
para utilizarlas en el modelado de objetos es hacer que la función
F(x,y,z) sea la suma de varias contribuciones generadas por diferentes
objetos básicos instanciados en la escena, normalmente
esferas o elipsoides. El símil físico sería
que cada uno de esos objetos genera un cierto campo de fuerza
(gravitatorio, eléctrico...), un potencial a su alrededor,
en cada punto del espacio. La superficie equipotencial envolverá
a los objetos básicos como una película elástica
de aspecto suave. Es por ello que estos 'objetos globulares' (blobs
o blobby objects) que se utilizan ampliamente para representar
formas orgánicas, en las que la piel o la concha recubren
las estructuras internas (esqueleto, músculos).
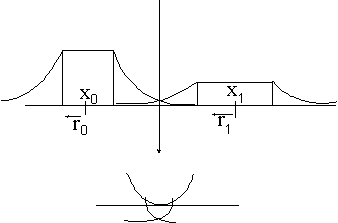
Un ejemplo popular de esta aproximación es
la combinación de funciones gaussianas en las que el potencial
en cada punto producido por cada una de las componentes es una
curva normal o gaussiana.
De este modo si para cada punto se define :
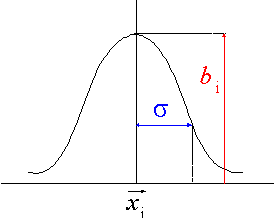

Entonces podemos definir el potencial en cada punto
como :
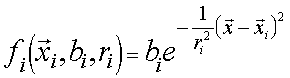
De forma que la superficie equipotencial quedaría
como sigue :
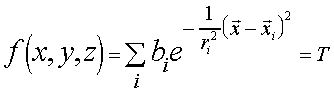
Este tipo de objetos se conoce también como
blobs en algunos paquetes de animación.
Otro son las metaballs, definidas mediante
polinomios, y por tanto más fáciles de evaluar,
como podemos ver en su ecuación general (ver figura 1.1.2.2).
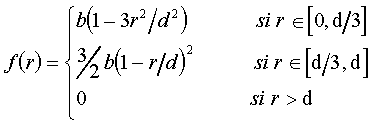
Con 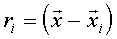
Otra posibilidad son los soft objects. En
los que la ecuación general es :
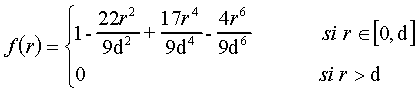

La visualización de cualquier isosuperficie
puede realizarse básicamente por dos métodos diferentes,
bien por generación de polígonos ("marching.htm">Marching
Cubes ) o por trazado de rayos [ENLACE]. También pueden
dibujarse ciertas aproximaciones durante la fase de modelado,
que requiere una visualización rápida [ENLACE] "aprox_edit.htm"
Aproximaciones durante la edición.
Deberemos representar nuestros objetos con un modelo
de sólido cuando:
Existen dos tipos básicos de representaciones:
Al igual que en las superficies formadas por polígonos
podían plantear situaciones no regulares, también
las representaciones de volumen pueden dar lugar a singularidades
(p. ej. objetos de volumen nulo) o incoherencias (p. ej. autointersecciones
en las que una misma parte del objeto se representa dos veces).
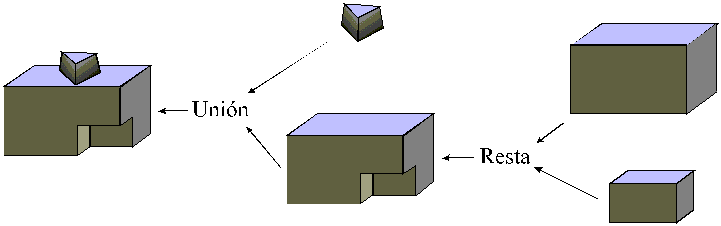
Sea cual sea el modelo que elijamos para representar los sólidos, éste debe permitirnos realizar las llamadas operaciones booleanas (unión, intersección, resta o negación).
[NOTA: La resta y la negación son interdefinibles,
es decir, que podemos definir una a partir de la otra del siguiente
modo :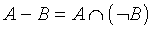
Estas operaciones deben definirse de forma que sean
regulares: su resultado debe ser siempre un sólido real
(deben tratarse con cuidado los casos en que la intersección
es sólo un plano, recta o punto, o cuando el resultado
puede ser nulo, por ejemplo al restar un objeto a sí mismo).
Estas operaciones son muy útiles para el modelado geométrico
3D, ya que podemos crear nuevos objetos añadiendo o quitando
partes sólidas manteniendo la unidad del objeto como entidad.
Debemos tener siempre presente que cada método
de representación tiene ciertas ventajas e inconvenientes,
por lo que se suelen combinar en las aplicaciones prácticas.
Por ejemplo, se puede usar uno durante la fase de modelado, otro
para una simulación física y otro para la visualización
realista, efectuándose las conversiones apropiadas.
Los objetos de partida pueden generarse por diferentes
métodos, sea cual sea el método de representación
interna elegido. Los más sencillos son la instanciación
de primitivas, es decir, de objetos predefinidos, y la generación
por desplazamiento de superficies o sólidos. El barrido
o desplazamiento puede ser utilizado también como una representación
de ciertos objetos. Por ejemplo, cuando trasladamos una figura
plana a lo largo de un eje definimos una forma tridimensional
por extrusión (ver figura 1.2.1.) y cuando giramos una
superficie o línea en el espacio alrededor de un eje definimos
un sólido de revolución.
a) Extrusión de una superficie (genera un
volumen)
Ex. paralela recta
Ex. paralela curva

Ex. de proyección: convergente o divergente

Ex. Generalizada
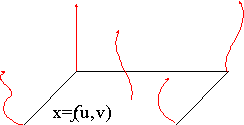
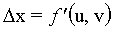
b) Extrusión de una línea
Existen los mismos tipos que en el caso anterior.
La línea puede ser abierta o cerrada dependiendo
de lo cual se generará una superficie abierta o cerrada
(que envuelve un volumen).
c) Rotación de una línea sobre su eje
Genera una superficie o un sólido de revolución
dependiendo de si la línea se cierra sobre su eje (ver
figura 1.2.1.)
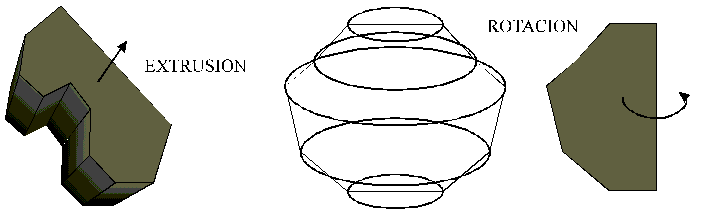
El mecanismo de barrido se suele emplear para construir
los objetos, pero a la hora de visualizarlos lo habitual es pasar
a otro tipo de representación (paramétrica o poligonal).
Sin embargo, también es posible hacer un trazado de rayos
con bastante facilidad.
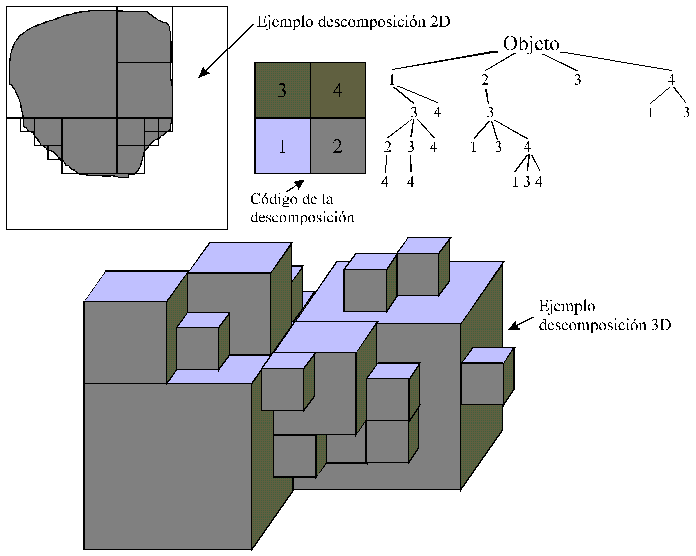
1.2.2. DISEÑO DE SÓLIDOS. GEOMETRÍA
SÓLIDA CONSTRUCTIVA ( En inglés
CSG: Constructive Solid Geometry)
Este es uno de los paradigmas dominantes en el modelado
de sólidos. Se trata de instanciar objetos primitivos y
combinarlos mediante operaciones booleanas ( unión, intersección,
resta, ...). La representación de un objeto complejo es
un árbol en el que figuran las operaciones y objetos primtivos
que definen la forma del objeto (ver figura 1.2.2.). De esta forma
tan sencilla se representa un objeto en la memoria o en una base
de datos.
En el árbol CSG se incluyen distintos tipos
de nodos :
La cuestión siguiente es cómo visualizarlo.
Existen algoritmos que sirven para visualizar directamente el
objeto a partir del árbol CSG. mediante [ENLACE] trazado
de rayos o procesamiento de tipo ráster. Otros métodos
se basan en el paso de la representación CSG a otro tipo
(superficie o partición espacial) que facilite el uso
de algoritmos de visualización.
Como otros métodos de representación
del volumen, el sistema CSG resulta también adecuado para
añadir a los objetos propiedades físicas, ya que
se está representando directamente su volumen, y permite
realizar la comprobación de pertenencia al objeto de los
puntos en el espacio, como vamos a ver ahora.
El modelo CSG resulta muy adecuado cuando los objetos
a representar se forman por combinación de formas básicas
sencillas (paralelepípedos, esferas, cilindros, etc.),
pero puede resultar muy ineficiente para otro tipo de objetos.
C.S.G. como método de partición
espacial
Los métodos de partición espacial distinguen
entre aquellas regiones del espacio que contienen puntos del objeto
y aquellas que no lo contienen. La evaluación de puntos
resulta muy sencilla en un árbol CSG por medio de un proceso
recursivo.
El algoritmo siguiente muestra una posible implementación
para este algoritmo recursivo suponiendo que la estructura NODO
tiene una serie de campos específicos como son, nodo_tipo
que indica el tipo de operación booleana , si es un nodo
de operación, o el tipo de objeto en caso de que se trate
de un nodo de primitivas. Además contiene dos campos adicionales
entendidos como dos punteros a cada uno de sus posibles hijos,
que serán de nuevo una estructura nodo.
esta_dentro (nodo, punto)
{
switch (nodo_tipo) {
caso UNION : esta_dentro esta_dentro (nodo.hijo1) OR esta_dentro(nodo.hijo2)
caso INTERSEC :esta_dentro esta_dentro(nodo.hijo1) AND esta_dentro(nodo.hijo2)
caso RESTA: esta_dentro esta_dentro (nodo.hijo1) AND NOT esta_dentro(nodo.hijo2)
.
.
.
caso CUBO : esta_dentro comprobar_cubo(punto)
.
.
.
1.2.3. MODELOS DE PARTICIÓN ESPACIAL
Aunque la geometría sólida constructiva
induce una división del espacio, no puede hablarse propiamente
de una partición, ya que por definición ésta
estaría formada por elementos que no tienen intersección
entre sí.
Definición de partición espacial: Conjunto
de volúmenes { Vi } , que permite caracterizar qué
parte del espacio está dentro del objeto y qué
parte está fuera. Debe cumplir:
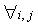
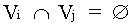
Algunas de las utilidades del empleo de este método
de representación son:
a) Clasificación de puntos : para discernir cuáles son los puntos del espacio ocupados por el objeto y cuáles no

b) Información sobre propiedades de puntos
en el espacio. Cada volumen de la partición puede además
contener información adicional sobre alguna propiedad del
objeto en esa parte del espacio (densidad, color, presión,
composición…).
c) Clasificación de objetos dentro de la escena
: en este caso no se trataría de describir la forma de
un objeto determinado, sino de agrupar los objetos de una escena
compleja en partes para optimizar los métodos de visualización
[ENLACE OPTIMIZACION TRAZADO RAYOS], [ENLACE OPTIMIZACION TIEMPO
REAL].
Las particiones pueden dividirse en no jerárquicas,
cuando existe un único conjunto de volúmenes que
forman la partición, y no tiene relaciones internas de
inclusión, o bien particiones jerárquica y que
consistirán en sucesivas particiones de más y más
detalle, cuyos volúmenes están incluidos en una
partición de nivel inferior, y que se forma mediante operaciones
sucesivas de división.
1.2.3.1. PARTICIONES NO JERÁRQUICAS
En este caso la partición no se forma por
operaciones sucesivas de división, sino que se da directamente
todo el conjunto de volúmenes en los que se ha dividido
el espacio de partida. No existen relaciones de inclusión,
entre los volúmenes .
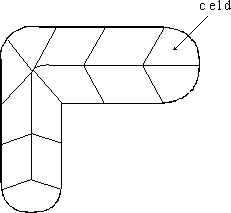
* Descomposición en celdas [dibujo]
En este caso los volúmenes de la partición
son celdas contiguas delimitadas por caras que pueden ser planas
o curvas, y que pueden tener asociados datos escalares o vectoriales
sobre la parte del objeto que representan. Las diferentes celdas
se encuentran pegadas entre sí sin intersectarse, y pueden
tener diferente forma y tamaño. Frecuentemente esta representación
se usa para efectuar el llamado análisis por elementos
finitos (FEA: Finite Element Analysis), que simula
efectos físicos en un objeto sólido o fluido (cambios
de temperatura, presión, velocidad de flujo, etc.) utilizando
una descomposición en celdas que interactúan entre
sí.
Aunque se trata de una estructura de datos sencilla,
tiene el inconveniente de requerir gran volumen de almacenamiento.
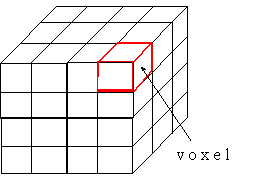
* Enumeración de la ocupación espacial:
voxels [dibujo]
Es un caso especial de descomposición por
celdas en el que éstas son todas idénticas y se
organizan en un entramado regular o rejilla. Es frecuente que
las celdas sean pequeños cubos alineados en una trama ortogonal
en cada uno de los ejes de coordenadas. Estas celdas idénticas
se llaman voxels (el equivalente de un pixel en tres dimensiones).
Se trata de una representación muy utilizada para almacenar
datos de dispositivos tipo escáner. El problema es la cantidad
de espacio que se requiere para almacenar un objeto complejo y
el coste de su representación visual.
1.2.3.2. PARTICIONES JERÁRQUICAS
Este tipo de particiones se caracteriza por irse
realizando por niveles sucesivos. La estructura de datos que se
emplea es un árbol, lo que disminuye el espacio de almacenamiento
requerido y hace posible definir a la vez varios niveles de detalle.
Podremos acceder a la información o efectuar la visualización
recorriendo la estructura solamente hasta el nivel que nos interese.
* Particiones Jerárquicas no ortogonales:
árboles binarios
Se puede efectuar una división sucesiva del
espacio en semiespacios utilizando planos de orientación
arbitraria. Estos planos se organizan en un árbol de
particiones espaciales binarias o BSP-tree (Binary
Space Partition tree), en el que cada nodo representa un plano,
y sus dos hijos son los dos semiespacios que define. En los nodos
terminales del árbol del árbol se nos indica si
cada región definida por los sucesivos cortes cae dentro
o fuera del objeto (ver un ejemplo en 2D en la figura 1.2.3.2).
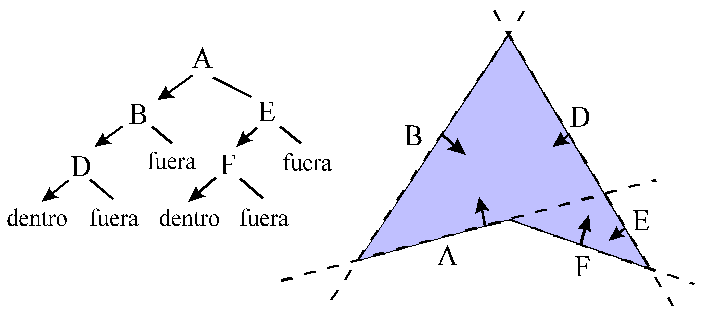
Utilización de un BSP_trees para clasificar
puntos
Como los demás métodos de partición
espacial, estos árboles binarios nos permiten efectuar
una clasificación de la pertenencia de cualquier punto
del espacio al objeto definido. Para ello hay que comenzar por
el plano que está en el nodo raíz del árbol.
Calculando el signo de la distancia del punto al plano se sabe
si hay que pasar a la rama derecha o la izquierda del árbol.
Se sigue este proceso recursivamente hasta que se llega a un nodo
terminal, que nos indicará si el punto está dentro
o fuera.
esta_dentro (nodo, punto)
{
si ( nodo = SI ) esta_dentro VERDAD /* Nodo terminal "dentro" = SI */
si ( nodo = NO ) esta_dentro FALSO /* Nodo terminal "fuera" = NO */
si ( comprobar_punto_plano ( punto, nodo.plano) = DENTRO )
esta_dentro esta_dentro (nodo.nodo_dentro, punto) /* Pasar a hijo izquierdo */
sino
esta_dentro esta_dentro (nodo.nodo_fuera, punto) /* Pasar a hijo derecho */
El problema es que la representación de un
objeto con un BSP-tree no tiene porqué ser única,
y por lo tanto las hay más sencillas y más complejas.
Por esta razón habrá que tener cuidado con el orden
que se emplea al efectuar las particiones. Las mejores elecciones
serán posiblemente aquellas que descarten más espacio
que no pertenecen al objeto.
Además de las utilidades comunes a todos los
métodos de partición, los árboles binarios
han sido frecuentemente utilizados para ordenar los polígonos
de una escena según la distancia al observador, y poder
de esa manera aplicar el algoritmo del pintor (dibujar los polígonos
de mayor a menor distancia) para calcular la ocultación
de superficies en una escena 3D.
Para visualizar este tipo de objetos podemos emplear
el trazado de rayos o bien convertirlos primero en polígonos.
Como puede verse fácilmente, los árboles
binarios de particiones resultan especialmente eficientes para
representar objetos formados por facetas planas, en los que la
representación resulta, además, exacta.
* Particiones jerárquicas ortogonales (según
los ejes del espacio)
En este caso las sucesivas particiones se realizan
según planos que están orientados siguiendo los
ejes ortogonales del espacio. El espacio suele, en este caso,
delimitarse mediante una caja ortogonal que contiene completamente
al objeto o escena. Si cada partición divide al espacio
en dos semiespacios iguales, entonces estaríamos de nuevo
ante un árbol binario. Si cada partición divide
la caja en cuatro partes iguales de forma recursiva, entonces
tenemos un árbol de cuadrantes o quadtree (ver
figura 1.2.3.2.1.), que se suele usar para figuras planas. En
el espacio resulta conveniente la división de cada caja
en ocho cajas de tamaño mitad, formándose un árbol
de octantes u octree.
Las particiones también pueden ser no homoeneas,
cuando las partes resultantes no son iguales.
a) Partición jerárquica ortogonal homogénea:
Octrees
Si queremos describir la forma de un objeto con un
octree o árbol de octantes tenemos que crear una estructura
arbórea en la que la que el volumen ocupado por el objeto
se va aproximando recursivamente por medio de cubos, o paralelepípedos
en general. Se trata de combinar celdas ortogonales cuya longitud
de arista se va dividiendo sucesivamente por 2, intentando rellenar
lo más aproximadamente posible el espacio del objeto deseado
[VER DIBUJO DONDE SE EXPLICA LA FORMACION PROGRESIVA DEL OCTREE
ver figura 1.2.3.2.1.]. Los nodos que no caen totalmente dentro
o fuera del objeto se seguirán subdividiendo de forma recursiva.
En cada nodo del árbol se puede indicar únicamente
si la celda correspondiente cae dentro o fuera del objeto, o se
puede considerar algún tipo de gradación (parcialmente
dentro, 25, 50 y 75 % dentro, etc.). La recursión deberá
detenerse según algún criterio (por ejemplo, las
celdas no pueden tener una arista menor de un cierto valor) se
limita directamente la profundidad del árbol a un valor
máximo.
Existen métodos para asociar un código
a cada posible celda, de manera que exista una notación
para enumerar las que componen un cierto objeto.
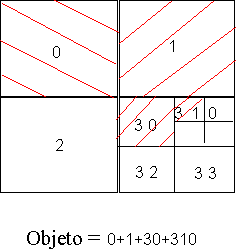
La primera llamada al función tomaría como parámetros el cubo que se va a ir dividiendo y el valor del umbral para el cual ya no se deberá seguir dividiendo. La función conectar_nodo añade a la estructura arborescente el nuevo nodo, de tal forma que ya se conoce el camino desde la raíz hasta este nodo.
poner_nodo (nodo_padre, real lado, real lado_minimo)
{
si lado > lado_minimo
{
para cada octante o cuadrante
si (octante objeto)
{
hijo crear_nodo (SI)
conectar_nodo (padre, hijo)
sino si ( octante objeto)
{
hijo crear_nodo (NO)
conectar_nodo (padre, hijo)
sino
{
hijo crear_nodo (INDETERMINADO)
conectar_nodo (padre, hijo)
poner_nodo ( hijo, lado/2, lado_minimo)
En el caso de los octrees también resulta
fácil utilizar esta estructura para clasificar puntos,
comprobando recursivamente la pertenencia del punto a los nodos
del árbol, comenzando por el nodo raíz.
b) Particiones jerárquicas ortogonales no
homogéneas
En este caso la descomposición no se realiza
por mitades iguales sino desplazando los planos de corte al punto
donde se considere óptimo. De esta forma se puede aproximar
más rápidamente la forma del objeto, aunque la estructura
de datos se complica ligeramente y resulta un poco más
difícil de manejar.
Los métodos jerárquicos ortogonales
tienen la ventaja de presentar una estructura de datos muy compacta,
que se presta a la utilización de algoritmos recursivos
muy sencillos. Al ser jerárquicas, permiten una representación
multiresolución del objeto y resultan mucho más
compactas que la enumeración espacial (voxels).
Por contra, resulta difícil llegar a representar
a un objeto de forma exacta, ya que éstos raramente tienen
todas sus facetas orientadas ortogonalmente. La visualización
de un objeto representado por un octree también es difícil,
puesto que la transformación en polígonos no es
inmediata, y el trazado de rayos tampoco es fácil si queremos
calcular el valor del vector normal en la superficie del objeto
para efectuar la iluminación.