PRÁCTICAS CURSO 1996-97
1º INGENIERÍA INFORMÁTICA
|
LABORATORIO DE ESTRUCTURAS DE DATOS PRÁCTICAS CURSO 1996-97 1º INGENIERÍA INFORMÁTICA |
|
Realizar un programa que pida al usuario la altura y el radio de un cilindro y determine su área y su volumen.
Ejercicio 2
Escribir un programa que pida el lado de un cuadrado y muestre el valor de su área y su perímetro
Ejercicio 3
Calcular la media de tres números introducidos por teclado, sin utilizar sentencias repetitivas.
Ejercicio 4
Realizar un programa que calcule el área de un triángulo mediante la utilización de la fórmula de Herón:
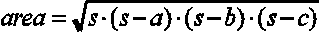donde: a, b y c son los lados del triángulo, y
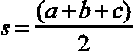
Realizar un programa que determine el valor máximo y el valor mínimo de un conjunto de tres valores, sin utilizar sentencias repetitivas.
Ejercicio 6
Realizar un algoritmo que averigüe si un número es par o impar.
Ejercicio 7
Realizar un programa que calcule las raíces de una ecuación de segundo grado, dando todas las posibles soluciones (incluidas las soluciones complejas)
Ejercicio 8
Diseñar un algoritmo que determine el precio de un billete de ida y vuelta en ferrocarril, dando la distancia a recorrer y el número de días en destino, sabiendo que si la estancia es superior a 7 días y la distancia es superior a 800 km. el billete tiene una reducción del 30%. El precio por kilómetro es de 8,5 pts.
Realizar un programa que muestre por pantalla la tabla de multiplicar del dos. Hacer tres versiones utilizando en cada una de ellas cada una de las estructuras repetitivas (desde...hasta (For..To..), hacer...mientras/repetir...hasta (Repeat...Until...), mientras...hacer (Do...While...)).
Ejercicio 10
1. Calcular, utilizando los tres tipos de estructuras repetitivas:
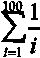
2. Calcular:
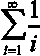con un error menor que 0,003
Ejercicio 11
1. Realizar un programa que escriba el cubo de los números del 1 al 20
2. Realizar un programa que escriba el cubo de los números naturales tales que el cubo tenga como máximo cuatro cifras.
3. Realizar un programa que escriba el cubo de los números naturales tales que el cubo tenga exactamente cuatro cifras.
Ejercicio 12
Realizar un programa que calcule el factorial de un número dado introducido por teclado, sin utilizar funciones.
Ejercicio 13
Dada la serie de números naturales de Fibonacci:
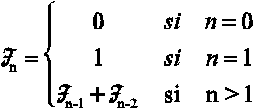
realizar un programa que pida un número natural y calcule el elemento de la serie de Fibonacci asociado a él, sin utilizar funciones ni procedimientos.
Ejercicio 14
Realizar un programa que calcule la potencia de un número real elevado a un número natural, sin utilizar ni funciones ni procedimientos.
Ejercicio 15
Realizar un programa que calcule los valores del polinomio de Legendre de forma iterativa para un valor `x' y un grado `n' determinados, definido el polinomio de Legendre como:
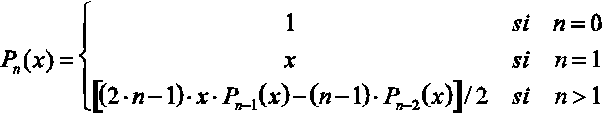Ejercicio 16
Realizar un programa que muestre los valores de todas las piezas del domino de forma ordenada:
0-0
0-1 1-1
0-2 1-2 2-2
...
Ejercicio 17
Realizar un programa que determine el valor del cociente y el resto de una división entre números enteros.
Ejercicio 18
Escribir una función en pseudocódigo que calcule una integral definida, mediante el método numérico de los rectángulos. El usuario deberá introducir los límites de la integral y el número de intervalos con que quiere trabajar, y la función devolverá el valor de la integral. Supondremos la integral de una función genérica f(x).
Implementar los ejercicios 12, 13, 14, 15 y 17, del bloque c.-, mediante la utilización de funciones o procedimientos recursivos.
Ejercicio 20
Realizar un programa que determine recursivamente el elemento (x,y) de la función de Ackermann definida como una aplicación:
A: N2 -&mt N
que cumple las siguientes premisas:
(i) A(0, y) = y+1
(ii) A(x, 0) = A(x-1, 1)
(iii) A(x, y) = A(x-1, A(x, y-1))
El programa pedirá los valores `x' e `y' por teclado y mostrará el valor de la función de Ackermann en ese punto.
Ejercicio 21
Realizar un algoritmo que transforme un cierto número `n' en base diez, introducido por teclado, en el mismo número en base binaria, mediante la utiliación de un procedimiento recursivo.
Ejercicio 22 - Torres de Hanoi
En el templo de Benarés, a las orillas del Ganges, bajo la cúpula que marca el centro del mundo hay una lamina de metal con tres agujas de diamante. En una de ellas, Bramah, cuando creo el mundo, puso 64 discos de oro, de manera que el disco más grande estaba sobre la lámina de metal y el resto de discos de mayor a menor uno sobre otro. Día y noche, incesantemente, los monjes cambian de aguja los discos con unas reglas fijas: Sólo pueden mover cada vez un sólo disco; y nunca puede estar un disco más grande sobre uno más pequeño. Dice la leyenda que cuando los sesenta y cuatro discos hayan sido cambiados de aguja, los monjes se convertirán en polvo y el mundo desaparecerá con un gran estallido.
Se trata de realizar un algoritmo recursivo que, a partir de un número `n' de discos introducido por teclado, emule las funciones del monje y diga qué disco y en qué aguja hay que colocarlo en cada uno de los pasos de manera que lleve a cabo la tarea de cambiar los discos de aguja.
Opcionalmente, podría contarse el número de pasos que se realizan para llevar a cabo el intercambio, y los años que tardará en desaparecer el mundo si consideramos que el monje intercambia un disco por segundo.