PRÁCTICA Nş 6: 2 sesiones
(S7 y S8: del 17 al 28 de mayo 2004)
En los Bosques de Planilandia
Árboles binarios
0. Objetivo
El objetivo de esta práctica es aprender a implementar y utilizar el TAD Arbol binario.
1 Planilandia
Planilandia es un mundo-estado en donde todas las cosas tienen dos dimensiones y están contenidas en el espacio n 2. En particular, consideraremos una región de Planilandia de coordenadas positivas y menores o iguales que uno, en donde hay n ciudades.
El gobierno de Planilandia ha decidido instalar un sistema de telecomunicaciones para comunicar las n ciudades. La compañía Arbena (que como todo el mundo sabe pertenece a Ramavisión) se ha encargado de la instalación. El sistema consiste en la construcción de estaciones que comunican dos y sólo dos ciudades o estaciones, de manera que hay una estación principal en la que se encuentra el sistema en el que el presidente J. Arbust pretende implantar un sistema de espionaje y censura de mensajes.
Como todos los mensajes tienen que pasar por la estación principal, los costes del sistema dependen de (a) el número de estaciones desde la principal a cada ciudad y (b) de la distancia recorrida entre esos dos puntos. Por eso, en esta práctica se ha de calcular en que lugares se han de colocar las estaciones y qué tienen que conectar.
2. Desarrollo del programa
Trataremos en esta práctica de desarrollar un programa que nos determine la localización de las estaciones que comuniquen las diferentes ciudades y subestaciones.
La idea consiste en crear un árbol cuyos nodos contendrán o estaciones o ciudades (las ciudades serán hojas del árbol).
Inicialmente se tendrá un bosque de árboles, donde cada uno de los árboles contendrá un solo nodo con una ciudad.
La estrategia básica consiste en encontrar cual es el par de estaciones (raíces de los árboles contenidos en el bosque) que están más próximas, y construir en el punto medio de la recta que las une, una nueva estación repetidora que las conecte.
A partir de esta idea en cada iteración crearemos un nuevo árbol que contendrá como raíz la nueva estación y como subárboles los árboles cuyas estaciones conecta. Eliminaremos los árboles conectados del bosque e insertaremos el nuevo árbol en el bosque.
El algoritmo se detendrá cuando en el bosque quede un solo árbol.
3. Implementación de la práctica
El programa comenzará pidiendo el nombre del fichero de texto donde se encuentra la información topográfica de Planilandia. Este fichero contendrá en cada línea tres datos: Coordenada x de la ciudad y coordenada y de la ciudad, número de ciudades que se enlazan (1) y nombre de la ciudad tal y como se muestra en el ejemplo.
9.5012929e-01 5.7891305e-02 1 a1
A partir de esta información se creará el bosque con los árboles correspondientes a cada una de las ciudades.
Se recomienda guardar el bosque de árboles en un vector definido de la siguiente manera:
typedef Arbol VectorArbol[MAX];
struct Bosc
{
VectorArbol info;
int tam;
};
La información contenida en los nodos del árbol será la siguiente:
struct Node
{
float coordx, coordy; // posicio
string nom; // nom de la ciutat o estacio
int rep; // nombre de ciutats que connecta
};
Una vez generado el bosque se procederá a agrupar los diferentes árboles en un solo árbol mediante el algoritmo descrito en el apartado anterior.
Una vez agrupados todos los árboles se procederá a realizar unas sencillas estadísticas sobre el árbol, que se mostrarán por pantalla.
La información que hay que obtener del árbol es:
* Nombre de todas las estaciones, sus coordenadas y número de subestaciones que conectan.
* Número total de estaciones.
* Número medio de enlaces desde la estación principal (nodo raíz) hasta una ciudad.
* Número máximo de enlaces desde la estación principal (nodo raíz) hasta una ciudad.
* Longitud media de los enlaces.
* Longitud máxima de los enlaces.
Un posible resumen de resultados del programa podría ser:
estacio19 (0.603111 0.593958) connecta amb estacio18 i estacio14
estacio18 (0.425393 0.36275) connecta amb estacio17 i estacio16
estacio17 (0.689182 0.216583) connecta amb estacio15 i estacio13
estacio15 (0.887796 0.326529) connecta amb estacio11 i estacio3
estacio11 (0.856233 0.167934) connecta amb estacio5 i estacio4
estacio5 (0.920714 0.0983911) connecta amb a1 i a5
estacio4 (0.791752 0.237477) connecta amb a6 i a9
estacio3 (0.919359 0.485124) connecta amb a13 i a18
estacio13 (0.490568 0.106638) connecta amb estacio8 i estacio2
estacio8 (0.550707 0.0125676) connecta amb a4 i a11
estacio2 (0.430428 0.200708) connecta amb estacio1 i a19
estacio1 (0.450586 0.198768) connecta amb a7 i a10
estacio16 (0.161604 0.508916) connecta amb estacio12 i a8
estacio12 (0.304704 0.41404) connecta amb estacio6 i a16
estacio6 (0.203702 0.409431) connecta amb a2 i a15
estacio14 (0.780828 0.825166) connecta amb estacio10 i estacio9
estacio10 (0.672525 0.872491) connecta amb a3 i a14
estacio9 (0.889131 0.777842) connecta amb a17 i estacio7
estacio7 (0.842793 0.709462) connecta amb a20 i a12
Nombre total d'estacions: 19
Nombre mitj_a d'enlla_cos a ciutats: 4.75
Nombre m_axim d'enlla_cos a una ciutat: 6
Dist_ancia mitjana d'un enlla_c: 0.110694
Dist_ancia m_axima d'un enlla_c: 0.301578
Además de esta información que se mostrará por pantalla es interesante poder visualizar la información en algún programa de edición de gráficas (como por ejemplo gnuplot). Para ello se dará una función PintarArbre que recorre el árbol y genera un fichero que se puede visualizar de forma fácil con el editor de gráficos.
El prototipo de la función es:
void PintaArb(Arbol & , string);
A esta función se le pasa el árbol que queremos guardar en el fichero, y el nombre del fichero en el que queremos guardar la información.
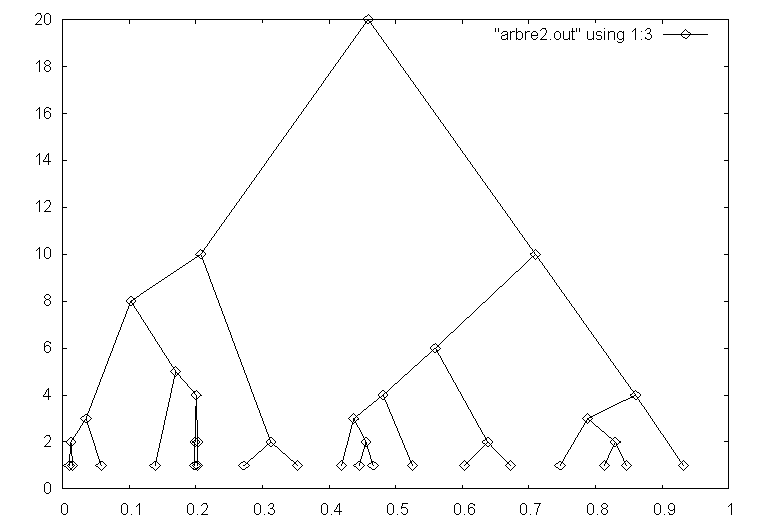
Utilizando el programa gnuplot podemos obtener las siguientes gráficas:
Si representamos en la coordenada x de la gráfica, la coordenada x de las ciudades y de las estaciones; y en la coordenada y de la gráfica, el número de ciudades conectadas por la estación (las ciudades conectan 0 ciudades) obtenemos:

Se puede representar también el plano de Planilandia o hacer una representación tridimensional de planilandia indicando en la coordenada z el número de ciudades conectadas por cada estación.
|
|
|
4. TAREA OPCIONAL
Se propone como tarea opcional realizar un algoritmo alternativo de agrupación de árboles.
Este algoritmo consiste en separar las n ciudades en dos mitades. Resolver el problema para cada una de las mitades. Esto nos proporcionará dos árboles con una subestación principal para cada una de las mitades. A partir de estos dos árboles, construiremos una nueva estación en el punto medio de la recta que separa las estaciones raíz de ambos árboles.
Es interesante comparar las estadísticas resultantes en cada uno de los algoritmos.
5. Requisitos
En esta práctica, habrá que entregar una documentación de programa completa para el programa principal, explicando el programa principal y las clases usadas.
Recordar que para poder acceder a la sesión de prácticas correspondiente es necesaria la entrega de la documentación del programa. Si no se presenta la documentación ANTES de acceder al laboratorio, no se permitirá la entrada a la sesión de prácticas.
6. Entrega
La práctica constará de tres módulos.
Dos módulos (##arbol.cpp y ##arbol.h) que contendrán los métodos y la interfaz de la clase árbol vista en clase y un módulo ##plani.cpp que contendrá las funciones necesarias de agrupación de árboles y creación de nuevas estaciones, así como las funciones de cálculo de estadísticas y gestión de ficheros.
La entrega puede realizarse por e-mail a la dirección del profesor encargado del grupo o en disquete al iniciar la siguiente sesión de prácticas, pero siempre ANTES de empezar la siguiente sesión de prácticas.
Cualquier práctica entregada fuera de plazo no será admitida para su corrección.
ENTREGA DE PROGRAMAS:
Al comenzar la sesión 9 de prácticas (31 de Mayo a 4 de Junio de 2004)
Referencias
Edwin A. Abbott. Planilandia Laertes, S.A. de Ediciones. Publicado por primera vez en 1884 como FLATLAND: A Romance of Many Dimensions con el seudónimo: A. Square. http://nedwww.ipac.caltech.edu/level5/Abbott/Abbott_contents.html